ロボットアームの逆運動学計算プログラム　　　 　 　　 　　　　 2001-01-25 改訂

（フォルダ名 ソースファイル 3-01-01Invtestsource (invtest4.c, SetInvvar.h, INVFUNC.h, calINV4.h） 2002-06-28 改訂

（テストの実行ファイル 3-0101Invtestexe） 2005-07-15 改訂

2016-01-06 改訂

［目次］

１． ファイル構成

２． ロボット構造の設定　　　

３． 座標変換行列

４． 初期ポーズから座標変換行列を計算　

５． calINV4.hにある解析プログラム

(０) 変換行列等の生成

(�T) 順運動学

(�U) 姿勢の逆運動学（ 解析的計算 ）

(�V) 位置の逆運動学（ 解析的計算 )

(�W) 位置姿勢の逆運動学（ 位置・姿勢逆運動学の繰り返し演算 ）

(�X) Newton法による位置姿勢の逆運動学

順運動学，及びワークの目標位置，目標姿勢を与えてそこに位置姿勢決めする逆運動学問題を解く．

ロボット諸元を設定して解を出力するプログラムの使用法を以下に述べる．

１．ファイル構成

１−１．１つのフォルダーに以下のファイルを組み入れる．

　main program(例えばここで用意したinvtest4.c)

SetInvVar.h

calInv4.h

FUNCALL.h

１−２．main programのinclude file を以下の順に設定する．:

#include “SetInvVar.h”

#include “INVFUNC.h”

#include “calINV4.h”

１−３．各ファイルの主な内容

・SetInvVar.h

　　main programと共通に使用する変数を定義．

・INVFUNC.h

ロボット解析に必要な基本演算（座標変換，一次／二次三角関数，４次方程式等）

初期ポーズから変換行列等を算出する EtoA()を含む．

・calINV4.h

　　順運動学計算 direct_kine3()…,，逆運動学計算 PInv4(), POInv8(),….等.

２ ．ロボット構造の設定

自由度n(=NFREE)，回転・直動関節の種別，軸の向きなどを設定する．

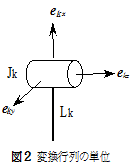
（１）関節・アームをベースから

B-(L1-J1)-(L2-J2)……(Ln-1-Jn-1)-(Ln-Jn)-Ln+1-Work)

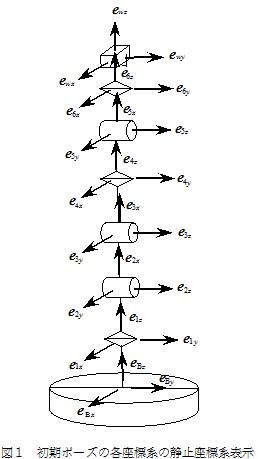
と名付ける．(図１ではn=6)

Bは静止座標の原点でなければならない．

（２）初期ポーズ（関節変位=0の状態）を基本とする．

（３）関節位置を各リンク座標の原点とする．

（４）回転関節軸をＺ軸とする．

（５）直動関節の場合はその方向をＸ軸とする．

（６）逆運動学解析のためのロボット構造の入力は

以下のようにする．初期状態で

（６−１）静止座標系から見たロボットのベース

位置：B（静止座標系の原点(0,0,0)）

（６−２）静止座標系から見た関節位置：Jk

（k=1,2,…..,n）

（６−３）静止座標系から見た各アーム座標系：Σk

（k=1,2,….., n）

（６−４）静止座標系から見たワークの位置：

（６−５）静止座標系から見たワークの姿勢：

（６−６）関節種別（回転Ｒか直動Ｓか）

図１の例では，

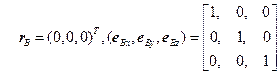
（静止座標の原点とする）

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．

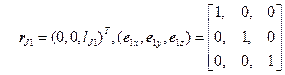
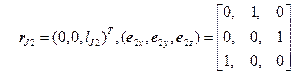
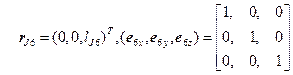
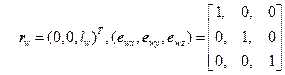
である.

静止座標系で表されたロボットポーズをフォルダーcalINV4.hにあるEtoA2()によって座標変換行列を作成する．

３．座標変換行列

座標変換行列は静変換行列と動変換行列の積Ak=Ask*Adkで表す．その配列順序に注意

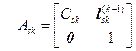
_{(k=1,2,…,n=NFREE)}

：Σk-1から見たΣksの姿勢（座標軸）

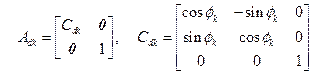
(Jk=’R’:回転関節)

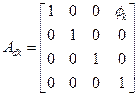　　 (Jk=’S’), (k=1,2,….,n=NFREE)

［註］行列の成分のプログラム中の表示は，

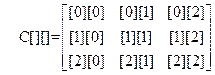
としている．

４．初期ポーズから座標変換行列を計算　

図１のように，初期ポーズを与え，EtoA2()によって座標変換行列等を生成する．

　・引数 (初期ポーズで設定すべき項目)

(k=1,2,…,NFREE+1):以下は初期ポーズの値を示す.

　　NFREE ：ロボットの自由度

　　IFTYPE[k]：Jkの関節タイプ　(=JTYPE[k]=’’R’or ‘S’）（‘RRRRRR’，’RSSRRR’など）

　　rJ0[k][3] ：関節Jkの位置のΣA表示

　　E0[k][3][3]：Σk座標系のΣA表示

　　rw[3] :ワークの位置のΣA表示 rJ0[Nw][3]で与える

　　Ew[3][3] :ワークの姿勢のΣA表示 E0[Nw][3][3]で与える．

　・戻し値：以下は関節変位q[ ]=0のときの値を示す．

　Cs[k][3][3]：Σsk→Σsk-1への静座標変換行列（Σsk-1から見たΣskの座標系）

Ls[k]　　 ：Jk-1→Jkリンク(アーム)LkのΣk-1表示）

ICs[k][3][3]：Cs[k][3][3]の逆行列（転置行列）

ILs[k][3] : Ls[k][3]のΣk表示

　　mm0[k][3] ：Ls[k][3]の方向ベクトル

　　llink[k] ：Ls[k][3]リンクの長さ

rwn[3], Ewn[3][3]：ワークの位置姿勢のΣn表示(=Ls[Nw][3])

　llinkrw ：Jn→Workの長さ(=Cs[Nw][3][3])

[註1] Nw=NFREE+1：ワークをNw番目の関節とみなす。

[註2] Cs[k][3]3[], rJ0[k][3],…、関節変位後はC[k][3][3], rJ[k][3],….と表す．

５．calINV4.hにある解析プログラム

// (０) 変換行列等の生成

// EtoA2( ) : ロボットの初期ポーズから変換行列等を生成する．(第4章)

// (�T) 順運動学

// direct_kine( ) : 関節角qs[ ]を与えて関節・ワークの位置姿勢を求める．

// direct_kineM( ) : 関節角qs[ ]を与えて指定したJ[M]の先のrM[3],EM[3][3]の位置姿勢を求める．

// (�U) 姿勢の逆運動学（解析的計算）

// calOinv2( ) : q[I, J, K]による対象姿勢の姿勢決め計算．最大2通りの解

// calOinv1( ) : 上記解の初期値に最も近い解を採用

// (�V) 位置の逆運動学（解析的計算)

// calPinv4( ) : q[I, J, K]による対象点の位置決め計算．最大4通りの解

// calPinv1( ) : 上記解の初期値に最も近い解を採用

// (�W) 位置姿勢の逆運動学：（位置決め・姿勢決めの繰り返し演算）

// calPOinv80( ) : (�U), (�V)の繰り返しによる位置姿勢決めの計算．最大８通りの解：引数qs[ ]を初期値とする．

// calPOinv81( ) : (�U), (�V)の繰り返しによる位置姿勢決めの計算．最大８通りの解：初期値qINT[8][ ]を自成する．

// calPOinv82( ) : (�U), (�V)の繰り返しによる位置姿勢決めの計算．最大８通りの解：初期値qINT[8][ ]を自成する．

// calPOinv83( ) : (�U), (�V)の繰り返しによる位置姿勢決めの計算．最大８通りの解：初期値qINT[8][ ]を自成する．

// calPOinv1( ) : 上記解の初期値に最も近い解のみを採用．

// calPOWRISTinv8( ) : リスト間アーム長=0のときの位置姿勢決め計算．繰り返しは1回．最大8通りの解

// calPOWRISTinv1( ) : 同上． 初期値に最も近い解を採用．

// [註] calPOinv1( )では(�U), (�V)の繰り返しで解が得られなければNewton法NewtonPO( )によって解を探す．

　・calPOinv80, 81, 82, 83( )の違いは後述

// (�X) Newton法による解法

// NewtonPO( ) : 6関節角による位置姿勢決めのNewton法．解は1通り

以下に各関数の取り扱いを説明する．

(０) 変換行列等の生成

EtoA2( ) : 第4章参照

(�T) 順運動学

　このファイルには順運動学計算プログラムも用意されている．

関節変位q[]を与えてそのときのポーズその他の結果を戻す．

（１−１）通常の順運動学：関節変位を与えて関節位置・ワークの位置姿勢等を求める。

void　 direct_kine( double q[ ] )

引数と戻す計算結果は以下の通りで，q[ ]以外は共通変数に分類している．

・引数 (k=1,2,…,NFREE+1)

q[k] : 関節変位

NFREE : 自由度

JTYPE[k] : ‘R’(回転関節)，=’S’(直動関節)

Cs[k][3][3] : 静変換行列

Ls[k][3] : JkのΣsk-1表示（Jk-1→JkベクトルのΣsk-1表示）

ICs[k][3][3] : Cs[k][]3[3]の逆行列(転置行列)

ILs[k][3] ; Ls[k][3]のΣks表示

mm0[k][3] : Ls[k][3]の方向ベクトル

rwn[3], Ewn[3][3] : ワークの位置姿勢のΣn表示

・戻し値

rJ[k][3] : 関節位置のΣA表示

C[k][3][3]=Cs[k][3][3]*Cd[k][3][3] : 変位後の変換行列

　IC[k][3][3] : C[k][3][3]の逆行列（転置行列）

Ld[k][3] : 変位後のJkのΣsk-1表示（変異後のJk-1→JkベクトルのΣk表示

　ILd[k][3] : Ld[k][3]のΣk表示

　ld[k][3] : 変位後の上記のΣA表示

　E[k][3][3] : ΣkのΣA表示

IE[k][3][3] : E[k][3][3]の逆行列(転置行列)

mm[k][3] : ld[k][3]の方向ベクトル(ΣA表示)

rw[3] : ワーク位置のΣA表示

　Ew[3][3] : ワーク姿勢のΣA表示

　IEw[3][3] : Ew[3][3]の逆行列

（１−２）中間のロボットアーム上の対象の位置姿勢を求める。

void direct_kineM( double qs[ ], int M, double rM[], double EM[3][3], double rMA[ ], double EMA[3][3] )

・引数

　上記共通変数

　qs[ ] : 関節変位

　M, rM[3], EM[3][3] : J[M]上の対象物の点と姿勢（ΣMs表示）

・戻し値

　rMA[3], EMA[3][3] : 変位後の対象の点と姿勢のΣA表示

・対象の姿勢計算の必要がなければダミーとして引数EM[3][3]は単位行列Iを指定するとよい。

(�U) 姿勢の逆運動学（ 解析的計算 ）

・以下の姿勢逆運動学演算は，関節J[M]の先の対象物を姿勢決めする問題となっている．

M=NFREEならば対象物はワークであり， EM ][3]=Ewn[ 3][3] である．

（２−１）J[M]の先の対象物の姿勢決め：2通りの解

int calOinv2( double qs[ ], int I, int J, int K, int M, double EM[3][3], double EG[3][3], double qqx[2][N] )

・引数 (k=1,2,…,NFREE)

qs[N] : 関節角の初期値

I, J, K : 姿勢決めする3関節角番号(I<J<K)

　　　　　 全て回転関節でなければならない．

M, EM[3][3] : ΣMs上の姿勢位置決めすべき対象姿勢

(自由度n=6でワークが対象ならばM=6, EM[3][3]=Ewn[3][3])

・戻し値

qqx[2][N] : 最大2通りの解

sol 解の数

（２−２）J[M]の先の対象物の姿勢決め：初期値q[ ]に近い1通りの解

int calOinv1( double qs[ ], int I, int J, int K, int M, double EM[3][3], double EG[3][3], double qO[ ] )

・引数 (k=1,2,…,NFREE)

qs[N] : 関節角の初期値

I, J, K : 姿勢決めする3関節角番号(I<J<K)

　　　　　 全て回転関節でなければならない．

M, EM[3][3] : ΣMs上の姿勢位置決めすべき対象姿勢

(自由度n=6でワークが対象ならばM=6, EM[3][3]=Ewn[3][3])

・戻し値

qO[N] : 初期値の最近解

sol : 解の数(0 or 1)

(�V) 位置の逆運動学（ 解析的計算 )

・以下の位置姿勢逆運動学演算は，関節J[M]の先の対象物を位置決めする問題となっている．

M=NFREEならば対象物はワークであり，rM[3]=rwn[3], EM ][3]=Ewn[ 3][3] である．

（３−１）位置の逆運動学１：最大4通りの解

int calPinv4( double qs[ ], int I, int J, int K, int M, double rM[ ], double EM[3][3],

double rG[ ], double qqx[4][N] )

・引数 (k=1,2,…,NFREE+1)

qs[k] : 関節角の初期値

I, J, K : 位置決めする3関節角番号(I<J<K)

M, rM[3] : ΣMs上の位置決めすべき対象点

(自由度n=6でワークが対象ならばM=6, rM[ ]=rwn[ ])

EM[3][3] : 同対象物の姿勢決めすべき姿勢（J[NFREE]を位置決めの対象とする場合に使う）

rG[3] : 位置決めの目標値（ΣA表示）

・戻し値

qqx[4][N] : 最大4通りの位置決め解

sol : 解の数

（３−２）位置の逆運動学２：初期値qs[ ]の最近値１通りの解

int calPinv1( double qs[ ], int I, int J, int K, int M, double rM[ ], double EM[3][3],

double rG[ ], double qP[ ] )

・引数 (k=1,2,…,NFREE)

qs[k] : 関節角の初期値

I, J, K : 位置決めする3関節角番号(I<J<K)

M, rM[3] : ΣMs上の位置決めすべき対象点

(自由度n=6でワークが対象ならばM=6, rM[ ]=rwn[ ])

EM[3][3] : 同対象物の姿勢決めすべき姿勢（J[NFREE]を位置決めの対象とする場合に使う）

rG[3] : 位置決めの目標値（ΣA表示）

・戻し値

qP[N] : 初期値の最近解

sol : 解の数(=0 or 1)

(�W) 位置姿勢の逆運動学（ 位置・姿勢逆運動学の繰り返し演算 ）

・以下の位置姿勢逆運動学演算は，関節J[M]の先の対象物を位置・姿勢決めする問題となっている．

M=NFREEならば対象物はワークであり，rM[3]=rwn[3], EM ][3]=Ewn[ 3][3 である．

（４−１）位置姿勢の逆運動学80：最大8通りの解

int calPOinv80( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qqx[8][N] )

・引数 (k=1,2,…,NFREE)

　qs[k]：関節角の初期値

　IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　(自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　rG[3], EG[3][3]：目標位置姿勢

・戻し値

　qqx[8][N]：最大8個の関節角解

　sol ：解の数

（４−２）位置姿勢の逆運動学81：最大8通りの解

int calPOinv81( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qqx[8][N] )

・引数 (k=1,2,…,NFREE)

　qs[k]：関節角の初期値

　IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　(自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　rG[3], EG[3][3]：目標位置姿勢

・戻し値

　qqx[8][N]：最大8個の関節角解

　sol ：解の数

（４−３）位置姿勢の逆運動学82：最大8通りの解

int calPOinv82( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qqx[8][N] )

・引数 (k=1,2,…,NFREE)

　qs[k]：関節角の初期値

　IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　(自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　rG[3], EG[3][3]：目標位置姿勢

・戻し値

　qqx[8][N]：最大8個の関節角解

　sol ：解の数

（４−４）位置姿勢の逆運動学83：最大8通りの解

int calPOinv83( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qqx[8][N] )

・引数 (k=1,2,…,NFREE)

　qs[k]：関節角の初期値

　IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　(自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　rG[3], EG[3][3]：目標位置姿勢

・戻し値

　qqx[8][N]：最大8個の関節角解

　sol ：解の数

（４−５）リストアーム長=0の場合の位置姿勢の逆運動学：最大8通りの解

　int calPOWRISTinv8( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qqx[8][N] )

・引数 (k=1,2,…,NFREE)

　 qs[k]：関節角の初期値

　 IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　 (自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　 rG[3], EG[3][3]：目標位置姿勢

・戻し値

　 qqx[8][N]：最大8個の関節角解

　 sol ：解の数

（４−６）位置姿勢の逆運動学１：初期値qs[ ]の最近値1通りの解

int calPOinv1( double qs[ ], int Ip , int Jp, int Kp, int Io, int Jo, int Ko,

int M, double rM[ ], double EM[3][3], double rG[ ], double EG[3][3], double qx[ ] )

・引数

qs[N] : 関節角の初期値

Ip, Jp, Kp : 位置決めする３関節角

Io, Jo, Ko : 姿勢決めする3関節角

M, rM[3], EM[3][3] : 位置姿勢決めする対象物のΣMs上の位置と姿勢(ΣMs表示)

rG[3], G[3][3] : 目標の位置と姿勢

・戻し値

　 qx[N] : 初期値の最近解

sol : 解の数(0 ro 1)

（４−７）リストアーム長=0の場合の位置姿勢の逆運動学W1：初期値[qs[ ] の最近値１通りの解

int calPOWRISTinv1( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qPOWR[ ] )

・引数 (k=1,2,…,NFREE)

　qs[k]：関節角の初期値

　IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　(自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　rG[3], EG[3][3]：目標位置姿勢

・戻し値

　qqx[8][N]：最大8個の関節角解

　sol ：解の数

(�X) Newton法による位置姿勢の逆運動学

char NewtonPO( double qs[ ], int IJK[ ], int M, double rM[ ], double EM[3][3],

double rG[ ], double EG[3][3], double qN[ ], double *errP, double *errO )

・引数 (k=1,2,…,NFREE)

　qs[k]：関節角の初期値

　IJK[6] : IJK[0, 1, 2]=[Ip, Jp, Kp]：位置逆運動学のための関節番号

IJK[3, 4, 5]=[Io, Jo, Ko]：姿勢逆運動学のための関節番号

M, rM[3], EM[3][3]：ΣMs上で定義した対象(ワーク)の位置と姿勢

　(自由度n=6でワークが対象ならばM=6, rM[3]=rwn[3], EM[3][3]=Ewn[3][3] )

　rG[3], EG[3][3]：目標位置姿勢

・戻し値

　qN[N]：関節角解

　sol ：解の有無 =’Y’:解あり，=’N’:解なし（漸近計算途中で特異点に陥った）

［参考１：位置決めの解析解法］

・calPinv4( )の解法は［参考文献］に記載されている．

・例外ケース

実際には記載の通常計算が適用できない例外ケースが多い．

　本プログラムcalPOinv4( )では考え得る全ての例外ケースの計算手順を含んでいる．

　詳細は添付資料のInvException.docx参照

・リストアーム長=0（L[Io+1〜Ko]=0）の場合

姿勢決め→位置決めの1回の計算で解を得ることができる．

［参考２：位置姿勢逆運動学解法の違い］

・calPOinv80, 81, 82, 83( )の違いは，位置決め・姿勢決め繰り返し演算の初期値の取り方の違いによる．

・逆運動学の解が存在するとして，解に到る収束の途は初期値qINT[ ]に大きく依存する．

　Newton法では解が遠ければ解へ辿り着くことはほとんど期待できない．

・できるだけ解に到る途があると思われる初期値qINT[ ]を設定する．

calPOinv80() : 通常のqs[ ]を初期値とし，［位置決め＋姿勢決め］の繰り返しを行う．

calPOinv81() : リストアーム長=0に縮め,た状態を初期状態とする．

位置姿勢決め計算の結果を初期値qINT[8][N]とする． (リストアーム長=0なので解が存在すれば必ず求まる)

　　　　　　　解がなければL[Kp+1]アームを伸ばして同様の計算をする．

　　　　　　　位置姿勢決め計算は初期ポーズから変更したアーム長を段階的に元に戻しながら位置姿勢決め解を求める，

　　　　　　　元に戻った時の最終解を解とする(最大8通り) ．

calPOinv82() : リストアーム長=0に縮め,た状態を初期状態とする．

位置姿勢決め計算の結果を初期値qINT[8][N]とする． (リストアーム長=0なので解が存在すれば必ず求まる)

　　　　　　　解がなければL[2〜Ko]アームを伸ばして同様の計算をする．

　　　　　　　位置姿勢決め計算は初期ポーズから変更したアーム長を段階的に元に戻しながら位置姿勢決め解を求める，

　　　　　　　元に戻った時の最終解を解とする(最大8通り) ．

calPOinv83() : 目標位置rG[3]を初期値qs[]のときの対象物(ワーク)位置rM0[3]方向へ位置姿勢決め解が存在するまで変更する．

　　　　　　　（rM0[3]が目標ならqs[ ]を含めた複数解が必ず存在する）

位置決め解が存在する位置姿勢決め複数解を初期ポーズ（ 初期値qINT[8][N] )とする．

初期ポーズから変更した目標を段階的に元に戻しながら位置姿勢決め解を求める，

　　　　　　　元に戻った時の最終解を解とする(最大8通り)．

・これらの計算であり得る全ての位置姿勢決め解が得られるというわけではない．

　どの方法が最善ということもない．それぞれ別の複数解を得る例がしばしばある．

［参考文献］

1. .“A new effective solution for inverse kinematics problem(synthesis) of a robot with any type of

configuration”, M. Takano, J of Fac. Eng., Univ. Tokyo(B), 38, 5 pp107-135, 1984.

２．「詳説ロボットの運動学」第４章，高野政晴，オーム社，2004.12.20