�@�@�@�U�D�@���{�b�g�A�[���̑��x�����x��� �@2004.10.05
�쐬
�\�[�X�t�@�C�� kineSource ���s�t�@�C�� kineexe
�@�@�@�@�@�Q�|�P�D���^���w�@�@�@�@ �@analys_pose( )
�@�@�@�@�@�Q�|�Q�D���x�����x��͂� �@analys_vel_acck( )
�@�@�@�@�@�Q�|�R�D���x�����x���A�@ analys_vel_accA( )
�@�@�@�@�@�Q�|�S�D���R�r�A��
Jacobian( )
�̉�͂��s���D
�P �D���{�b�g�\���̐ݒ�
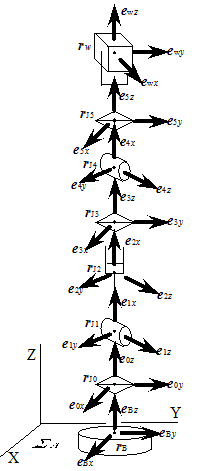 �i�P�j�߁E�A�[�����x�[�X����
�i�P�j�߁E�A�[�����x�[�X����
B-J0-L0-J1-L1-�c�cJn-1-Ln-1-Jn-Ln(Hand/Work)
�Ɩ��t����D(n=NFREE-1)
�i�Q�j������ԁi�ߕψʁ��O�̏�ԁj�� �@�@�@
��{�Ƃ���D
�i�R�j�߈ʒu���e�����N���W�̌��_�Ƃ���D
�i�S�j��]�ߎ����y���Ƃ���D
�i�T�j�����߂̏ꍇ�͂��̕������w���Ƃ���D
�i�U�j�t�^���w��͂̂��߂̃��{�b�g�\���̓��͂�
�ȉ��̂悤�ɂ���D������Ԃ� �@�@�@�@�@�@
�i�U�|�P�j�Î~���W�n���猩�����{�b�g�̃x�[�X
�ʒu�FB
�i�U�|�Q�j�Î~���W�n���猩���߈ʒu�FJk�@�@�@�@�@�@�@
�ik=0,1,�c..,n=NFREE-1�j
�i�U�|�R�j�Î~���W�n���猩���e�A�[�����W�n�F��k �@�@�@
�ik=0,1,�c.., n=NFREE-1�j
�i�U�|�S�j�Î~���W�n���猩�����[�N�̈ʒu�Frw
�i�U�|�T�j�Î~���W�n���猩�����[�N�̎p���F��w�@�@�@
�i�U�|�U�j�ߎ�ʁi��]�q�������r���j
�Q�D�O����
�@
�@���{�b�g�\���E���I�p�����[�^�� kinema.c �֎n���D�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���{�b�g�̏����|�[�Y
�@�@�@�@�iRRSRRR�̗�j
�m���n���W�ϊ��s��͐Õϊ��s��Ɠ��ϊ��s��̐ςŕ\���D���̔z���ɒ���
�@�@�@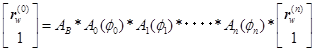 �C�@
�C�@![]()
(![]() )
)
�@�@�@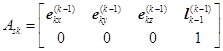 ��
��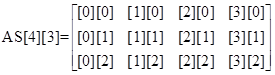
�@�@�@![]() �F��k-1���猩����sk�̎p��
�F��k-1���猩����sk�̎p��
�@�@�@![]() �F�����|�[�Y�̃A�[��
�F�����|�[�Y�̃A�[��![]() �x�N�g���̃�k-1�\��
�x�N�g���̃�k-1�\��
�@�@�@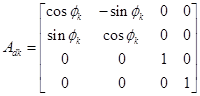 �@(
�@(![]() )�@�i
)�@�i![]() �j
�j
�@�@�@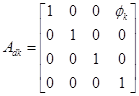 �@(
�@(![]() )�@��
)�@��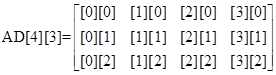
�i�Q�|�P�j�����`�Ԃ�����W�ϊ��s����v�Z����Ƃ��@
�}�̏�����Ԃ�^���č��W�ϊ��s������D
EtoA( NFREE, JTYPE,
BASP0, BASE0, rJ0, E0, As ) (2002-6-28, 2004-9-25 ����)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�����̊��Ɏn���ϐ�
�@�@int NFREE�F���{�b�g�̎��R�x
�@�@char JTYPE[k-th]�FJk�̊߃^�C�v�@(�eR�for �eS�f�j�i�eRRRRRR�f�C�fRRSRSR�f�Ȃǁj
�@�@double
BASP0[3]�F���{�b�g�x�[�X�̈ʒu�i��A�\���j
�@�@double
BASE0[3][3]�F���{�b�g�x�[�X�̎p���i��A�\���j
�@�@double rJ0[k-th][3]�F�ߓ_Jk�̏����|�[�Y�̈ʒu�i��A�\���j
�@�@double E0[k-th][3][3]�F�A�[��Lk�̏����|�[�Y�̎p���i��A�\���j
�@���߂��l
�@double As[k-th][4]3[]�F��k����k-1�ւ̐Í��W�ϊ��s��
��kinema.c�ɍ쐬����ϐ� ![]()
NFREE�F���R�x
JTYPE[k-th]�FJk�̊߃^�C�v(�eR�for �eS�f)
AB[4][3]�F��B����A�̍��W�ϊ��s��i���j
AS[k-th][4][3]�F�Í��W�ϊ��s��
WRKP0[3]�F���[�N�̃�n�\���̈ʒu(AS[NFREE][3-th)[3]�Ɠ����j
�@WRKXN[3]�CWRKYN[3],WRKZN[3]�F���[�N�̃�n�\���̎p���iAS[NFREE][0,1,2][3]�Ɠ����j
�i�Q�|�Q�j���ɍ��W�ϊ��s�������Ă���Ƃ�
setrobot( NFREE, JTYPE,
AB, As )
�����̊��Ɏn���ϐ�
�@�@int NFREE�F���{�b�g�̎��R�x(=6)
�@�@char JTYPE[k-th]�F��Jk�̃^�C�v�@�eR�f�܂��́eS�f(�eRRRRRR�f,�fRRSRSR�f�Ȃǁj
�@�@double
AB[4][3]�F��B����A�̍��W�ϊ��s��
�@�@double As[k-th][4][3]�F��k ����k-1�ւ̐Í��W�ϊ��s��(k=0,1,2,�c,NFREE-1)
�@�@double As[NFREE][4][3]�F��n�\���̃��[�N�̈ʒu�Ǝp��
�@���߂��l�@�Ȃ�
��kinema.c�ɍ쐬����ϐ�
NFREE�F���R�x
JTYPE[k-th]�F�߃^�C�v
AB[4][3]�F��B����A�̍��W�ϊ��s��i���j
AS[k-th][4][3]�F�Í��W�ϊ��s��iAs[k-th][4][3]�Ɠ����j
WRKP0[3]�F���[�N�̃�n�\���̈ʒu(As[NFREE][3-th)[3]�Ɠ����j
�@�@WRKXN[3]�CWRKYN[3],WRKZN[3]�F���[�N�̃�n�\���̎p���iAs[NFREE][0,1,2][3]�Ɠ����j
�R�D��͍���
�i�P�j���^���w
�@�@�@�ߕψ�����^���Ċe�߈ʒurJk�E�A�[���p��Ek�C���[�N�ʒurw�p��Ew������
��D
analys_pose(
PHI, RJ, EARM, RW, EW )
���v�Z�̂��߂ɕK�v�Ȋ��m�ϐ��ikinema.c�֊��Ɏn���Ă���ϐ��D�O�����ɂ��j
NFREE�F���R�x
As[k-th][4][3]�F�Í��W�ϊ��s��
As[NFREE-th][4][3]�F���[�N�̈ʒu�p���̃�n�\���in=NFREE-1�j
�����ւ̓���
double PHI[k]�F�ߕψ�(
rad or m )
�����̏o��
�@�@�@double RJ[k-th][3]�F�ߓ_Jk�̈ʒu�i��A�\���j(m)
�@�@�@double EARM[k-th][3][3]�F�A�[��Lk�̎p���i��A�\���j
�@�@�@double RW[3]�F���[�N�̈ʒu�i��A�\���j(m)
�@�@�@double EW[3][3]�F���[�N�̎p���i��A�\���j
�@�@�@
�i�Q�j���x�����x���k
�ߕψ�![]() �E���x
�E���x![]() �E�����x
�E�����x![]() �C�e�A�[���d�S�ʒurGk��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w�C����ъe�A�[���d�S�̑��xvGk�C�����xaGk�C���[�N�d�S�̑��xvGw�����xaGw���C��k���W�n�\���ŋ��߂�D
�C�e�A�[���d�S�ʒurGk��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w�C����ъe�A�[���d�S�̑��xvGk�C�����xaGk�C���[�N�d�S�̑��xvGw�����xaGw���C��k���W�n�\���ŋ��߂�D
�@�@�@analys_vel_acck(
PHI, DPHI, DDPHI, rg, OMEGA, ALPHA, VJ, AJ, VW, AW,
VG , AG, VGW, AGW )
���v�Z�̂��߂ɕK�v�Ȋ��m�ϐ��ikinema.c�֊��Ɏn���Ă���ϐ��D�O�����ɂ��j
NFREE�F���R�x
JTYPE[k-th]�FJk�̊߃^�C�v�i�fR�f or �eS�f �j
As[k-th][4][3]�F�Í��W�ϊ��s��
As[NFREE-th][4][3]�F���[�N�̈ʒu�p���̃�n�\���in=NFREE-1�j
�����ւ̓���
double PHI[k]�F�ߕψʁirad
or m�j
double DPHI[k]�F�ߑ��x(rad/s
or m/s)
double DDPHI[k]�F�߉����x(![]() or
or ![]() )
)
double
rg[k-th][3]�F�A�[��Lk�̏d�S�ʒu�i��k�\���j(m)
double
rg[n-th][3]�F�n���h�^���[�N�̏d�S�ʒu�i��n�\���j(m)(n=NFREE-1)
�@�@�����̏o�́@�iVW[], AW[]�ȊO�͑S�ă�k���W�n�\���j
�@�@�@double OMEGA[k-th][3]�F�A�[��Lk�̊p���x(rad/s)
�@�@�@double ALPHA[k-th][3]�F�A�[��Lk�̊p�����x(![]() )
)
�@�@�@double OMEGA[n-th][3]�F�n���h�^���[�N�̊p���x(rad/s) (n=NFREE-1)
�@�@�@double ALPHA[n-th][3]�F�n���h�^���[�N�̊p�����x(![]() )
)
�@�@�@double VJ[k-th][3]�F�ߓ_Jk�̑��x(m/s)
double
AJ[k-th][3]�F�ߓ_Jk�̉����x(![]() )
)
�@�@�@double VW[3]�F���[�NW�̑��x(m/s)
double AW[3]�F���[�NW�̉����x(![]() )
)
�@�@�@double VG[k-th][3]�F�A�[��Lk�d�S�̑��x(m/s)
double
AG[k-th][3]�F�A�[��Lk�d�S�̉����x![]() )
)
�@�@�@double VGW[3]�F�n���h�^���[�N�̏d�S�̑��x(m/s)�@�i��A�\���j
�@�@�@double AGW[3]�F�n���h�^���[�N�̏d�S�̉����x(![]() )�i��A�\���j
)�i��A�\���j
�i�R�j���x�����x���A
�@�@�@�i�Q�j�Ɠ����v�Z�ł��邪�C���ʂ���A�\���ŏo�͂���D
�ߕψ�![]() �E���x
�E���x![]() �E�����x
�E�����x![]() ��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w���C��A���W�n�\���ŋ��߂�D
��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w���C��A���W�n�\���ŋ��߂�D
�@�@�@analys_vel_accA(
PHI, DPHI, DDPHI, OMEGA, ALPHA, VJ, AJ, VW, AW )
���v�Z�̂��߂ɕK�v�Ȋ��m�ϐ��ikinema.c�֊��Ɏn���Ă���ϐ��D�O�����ɂ��j
NFREE�F���R�x
JTYPE[k-th]�FJk�̊߃^�C�v�i�fR�f or �eS�f �j
As[k-th][4][3]�F�Í��W�ϊ��s��
As[NFREE-th][4][3]�F���[�N�̈ʒu�p���̃�n�\���in=NFREE-1�j
�����ւ̓���
�@�@�@double OMEGA[k-th][3]�F�A�[��Lk�̊p���x(rad/s)
�@�@�@double ALPHA[k-th][3]�F�A�[��Lk�̊p�����x(![]() )
)
�@�@�@double OMEGA[n-th][3]�F�n���h�^���[�N�̊p���x(rad/s) (n=NFREE-1)
�@�@�@double ALPHA[n-th][3]�F�n���h�^���[�N�̊p�����x(![]() )
)
�@�@�@double VJ[k-th][3]�F�ߓ_Jk�̑��x(m/s)
double
AJ[k-th][3]�F�ߓ_Jk�̉����x(![]() )
)
�@�@�@double VW[3]�F���[�NW�̑��x(m/s)
double AW[3]�F���[�NW�̉����x(![]() )
)
�@�@�@double VG[k-th][3]�F�A�[��Lk�d�S�̑��x(m/s)
double
AG[k-th][3]�F�A�[��Lk�d�S�̉����x![]() )
)
�@�@�@double VGW[3]�F�n���h�^���[�N�̏d�S�̑��x(m/s)�@�i��A�\���j
�@�@�@double AGW[3]�F�n���h�^���[�N�̏d�S�̉����x(![]() )�i��A�\���j
)�i��A�\���j
�i�R�j���x�����x���A
�@�@�@�i�Q�j�Ɠ����v�Z�ł��邪�C���ʂ���A�\���ŏo�͂���D
�ߕψ�![]() �E���x
�E���x![]() �E�����x
�E�����x![]() ��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w���C��A���W�n�\���ŋ��߂�D
��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w���C��A���W�n�\���ŋ��߂�D
�@�@�@analys_vel_accA(
PHI, DPHI, DDPHI, OMEGA, ALPHA, VJ, AJ, VW, AW )
���v�Z�̂��߂ɕK�v�Ȋ��m�ϐ��ikinema.c�֊��Ɏn���Ă���ϐ��D�O�����ɂ��j
NFREE�F���R�x
JTYPE[k-th]�FJk�̊߃^�C�v�i�fR�f or �eS�f �j
As[k-th][4][3]�F�Í��W�ϊ��s��
As[NFREE-th][4][3]�F���[�N�̈ʒu�p���̃�n�\���in=NFREE-1�j
�����ւ̓���
double PHI[k]�F�ߕψʁirad
or m�j
double DPHI[k]�F�ߑ��x(rad/s
or m/s)
double DDPHI[k]�F�߉����x(![]() or
or ![]() )
)
double
rg[k-th][3]�F�A�[��Lk�̏d�S�ʒu�i��k�\���j(m)
double
rg[n-th][3]�F�n���h�^���[�N�̏d�S�ʒu�i��n�\���j(m)(n=NFREE-1)
�@�@�����̏o�́@�iVW[], AW[]�ȊO�͑S�ă�k���W�n�\���j
�@�@�@double OMEGA[k-th][3]�F�A�[��Lk�̊p���x(rad/s)
�@�@�@double ALPHA[k-th][3]�F�A�[��Lk�̊p�����x(![]() )
)
�@�@�@double OMEGA[n-th][3]�F�n���h�^���[�N�̊p���x(rad/s) (n=NFREE-1)
�@�@�@double ALPHA[n-th][3]�F�n���h�^���[�N�̊p�����x(![]() )
)
�@�@�@double VJ[k-th][3]�F�ߓ_Jk�̑��x(m/s)
double
AJ[k-th][3]�F�ߓ_Jk�̉����x(![]() )
)
�@�@�@double VW[3]�F���[�NW�̑��x(m/s)
double AW[3]�F���[�NW�̉����x(![]() )
)
�@�@�@double VG[k-th][3]�F�A�[��Lk�d�S�̑��x(m/s)
double
AG[k-th][3]�F�A�[��Lk�d�S�̉����x![]() )
)
�@�@�@double VGW[3]�F�n���h�^���[�N�̏d�S�̑��x(m/s)�@�i��A�\���j
�@�@�@double AGW[3]�F�n���h�^���[�N�̏d�S�̉����x(![]() )�i��A�\���j
)�i��A�\���j
�i�R�j���x�����x���A
�@�@�@�i�Q�j�Ɠ����v�Z�ł��邪�C���ʂ���A�\���ŏo�͂���D
�ߕψ�![]() �E���x
�E���x![]() �E�����x
�E�����x![]() ��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w���C��A���W�n�\���ŋ��߂�D
��^���āC�e�ߓ_�̑��xvJk�C�����xaJk�C�e�A�[���̊p���x��k�C�p�����x��k�C���[�N�̑��xvw�����xaw�C�p���x��w�p�����x��w���C��A���W�n�\���ŋ��߂�D
�@�@�@analys_vel_accA(
PHI, DPHI, DDPHI, OMEGA, ALPHA, VJ, AJ, VW, AW )
���v�Z�̂��߂ɕK�v�Ȋ��m�ϐ��ikinema.c�֊��Ɏn���Ă���ϐ��D�O�����ɂ��j
NFREE�F���R�x
JTYPE[k-th]�FJk�̊߃^�C�v�i�fR�f or �eS�f �j
As[k-th][4][3]�F�Í��W�ϊ��s��
As[NFREE-th][4][3]�F���[�N�̈ʒu�p���̃�n�\���in=NFREE-1�j
�����ւ̓���
double PHI[k]�F�ߕψʁirad
or m�j
double DPHI[k]�F�ߑ��x(rad/s
or m/s)
double DDPHI[k]�F�߉����x(![]() or
or ![]() )
)
�@�@�����̏o�́@�i�S�ă�k���W�n�\���j
�@�@�@double OMEGA[k-th][3]�F�A�[��Lk�̊p���x(rad/s)
�@�@�@double ALPHA[k-th][3]�F�A�[��Lk�̊p�����x(![]() )
)
�@�@�@double OMEGA[n-th][3]�F�n���h�^���[�N�̊p���x(rad/s) (n=NFREE-1)
�@�@�@double ALPHA[n-th][3]�F�n���h�^���[�N�̊p�����x(![]() )
)
�@�@�@double VJ[k-th][3]�F�ߓ_Jk�̑��x(m/s)
double
AJ[k-th][3]�F�ߓ_Jk�̉����x(![]() )
)
�@�@�@double VW[3]�F���[�NW�̑��x(m/s)
double AW[3]�F���[�NW�̉����x(![]() )
)
�i�S�j���R�r�A��
�@
�i�S�j���R�r�A��
�@�@�@�ߑ��x![]() �ƃ��[�N��̓_�̑��x�p���x��
�ƃ��[�N��̓_�̑��x�p���x��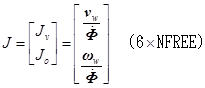 ��^����D
��^����D
Jacobian(
PHI, rp, JCBNV, JCBNO )
���v�Z�̂��߂ɕK�v�Ȋ��m�ϐ��ikinema.c�֊��Ɏn���Ă���ϐ��D�O�����ɂ��j
NFREE�F���R�x
JTYPE[k-th]�FJk�̊߃^�C�v�i�fR�f or �eS�f �j
As[k-th][4][3]�F�Í��W�ϊ��s��
As[NFREE-th][4][3]�F���[�N�̈ʒu�p���̃�n�\���in=NFREE-1�j
�����ւ̓���
double PHI[k-th]�F�ߕψ�
( rad or m )
�@�@�@double rp[3]�F���[�N��̓_�̃�n�\���@(m)
�@�@�����̏o��
�@�@�@double JCBNV[3][NFREE]�F=![]()
�@�@�@double JCBNO[3][NFREE]�F=![]()
�S �D�g�p�̒���
�i�P�j�^���w�̊����g���O��EtoA( )�܂���setrobot( )�̗\���v�Z���s���i���W�ϊ��s������߂邽�߁j�D
�P�x������v�Z����C���{�b�g�\���E���[�N�̈ʒu�p�����ς��Ȃ�����C����
��^���w�̊�������ł��g����D
�i�Q�jextern
int analys_pose( );
extern int analys_vel_acck( );
extern int analys_vel_accA( );
extern int EtoA( ); (�܂��́@setrobot( ); )
���`����D
�i�R�j�x�N�g���̔z���[0],[1],[2]�C�c�C�}�g���N�X[3][3]�̐����͑�P�s ([0][0] [1][0]
[2][0])�C��Q�s([0][1] [1][1] [2][1])�C��R�s([0][2]
[1][2] [2][2]) �̏���
�i�P�j�^���w�̊����g���O��EtoA( )�܂���setrobot( )�̗\���v�Z���s���i���W�ϊ��s������߂邽�߁j�D
�P�x������v�Z����C���{�b�g�\���E���[�N�̈ʒu�p�����ς��Ȃ�����C����
��^���w�̊�������ł��g����D
�i�Q�jextern
int analys_pose( );
extern int analys_vel_acck( );
extern int analys_vel_accA( );
extern int EtoA( ); (�܂��́@setrobot( ); )
���`����D
�i�R�j�x�N�g���̔z���[0],[1],[2]�C�c�C�}�g���N�X[3][3]�̐����͑�P�s ([0][0] [1][0]
[2][0])�C��Q�s([0][1] [1][1] [2][1])�C��R�s([0][2]
[1][2] [2][2]) �̏���
����D
�i�S�j ��J0 �̕ψʂ�PHI[0]�CJ1 �̊ߕψʂ�PHI[1]�CJ2 �̕ψʂ�PHI[2]�C�D�D�D��
����D
�i�T�jE[3][3] = (ex, ey, ez)�́CE[0-th][3] = ex, E[1st][3] = ey, E[2nd][3] = ez�ł���D
�m�Q�l�n
�@�g�p���ktest.c���Q�Ƃ̂��ƁD
�m�Q�l�����n
�u�ڐ����{�b�g�̉^���w�v�C���쐭���C�I�[���ЁC2004�D