Ⅲ． ロボットアームの動力学解析 2004.10.05 作成
ソースファイル robdynamicsSource 実行ファイル robdynamicsexe
３－１．逆動力学 inv_dynamics( )
３－２．動力学各項 dynamics_term( )
３－３．順動力学 direct_dynamics( )
３－４．動的運動解析 dynamic_motion( )
の解析を行う．
また，速度・加速度解析(kinema.c)も含まれているので，Ⅱ．速度加速度解析もできる．
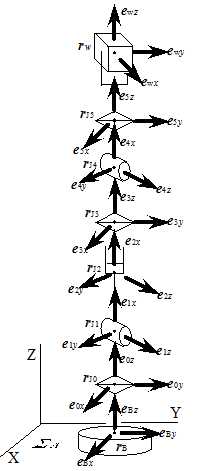１ ．ロボット構造の設定
（１）関節・アームをベースから
B-J0-L0-J1-L1-……Jn-1-Ln-1-Jn-Ln(Hand/Work)
と名付ける．(n=NFREE-1)
（２）初期状態（関節変位＝０の状態）を
基本とする．
（３）関節位置を各リンク座標の原点とする．
（４）回転関節軸をＺ軸とする．
（５）直動関節の場合はその方向をＸ軸とする．
（６）逆運動学解析のためのロボット構造の入力は
以下のようにする．初期状態で
（６－１）静止座標系から見たロボットのベース
位置：B
（６－２）静止座標系から見た関節位置：Jk
（k=0,1,…..,NFREE-1）
（６－３）静止座標系から見た各アーム座標系：Σk
（k=0,1,…..,NFREE-1）
（６－４）静止座標系から見たワークの位置：rw
（６－５）静止座標系から見たワークの姿勢：Σw
（６－６）関節種別（回転Ｒか直動Ｓか）
２．前準備
ロボットの初期ポーズ
ロボット構造・動的パラメータを dynamics.c へ受け渡す． （RRSRRRの例）
［註］座標変換行列は静変換行列と動変換行列の積で表す．その配列順序に注意
， 
(
)
⇒
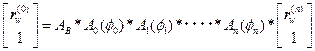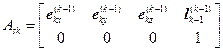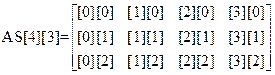
：Σk-1から見たΣskの姿勢
：初期ポーズのアーム
ベクトルのΣk-1表示
(
) （
）
(
) ⇒
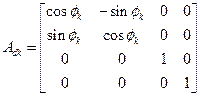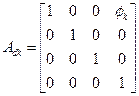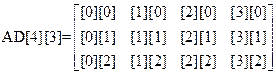
（２－１）初期形態から座標変換行列を計算するとき
図の初期状態を与えて座標変換行列を作る．
EtoA(NFREE,
JTYPE, BASP0, BASE0, rJ0, E0, As) (2002-6-28, 2004-9-25 改訂)
●この関数に受け渡す変数
int NFREE：ロボットの自由度
char JTYPE[k-th]：Jkの関節タイプ (‘R’or ‘S’）（‘RRRRRR’，’RRSRSR’など）
double BASP0[3]：ロボットベースの位置（ΣA表示）
double BASE0[3][3]：ロボットベースの姿勢（ΣA表示）
double rJ0[k-th][3]：関節点Jkの初期ポーズの位置（ΣA表示）
double E0[k-th][3][3]：アームLkの初期ポーズの姿勢（ΣA表示）
●戻し値
double As[k-th][4]3[]：Σk→Σk-1への静座標変換行列
●dynamics.cに作成する変数 
NFREE：自由度
JTYPE[k-th]：Jkの関節タイプ(‘R’or ‘S’)
AB[4][3]：ΣB→ΣAの座標変換行列（一定）
AS[k-th][4][3]：静座標変換行列
WRKP0[3]：ワークのΣn表示の位置(AS[NFREE][3-th)[3]と同じ）
WRKXN[3]，WRKYN[3],WRKZN[3]：ワークのΣn表示の姿勢（AS[NFREE][0,1,2][3]と同じ）
（２－２）既に座標変換行列が分かっているとき
setrobot(NFREE,
●この関数に受け渡す変数
int NFREE：ロボットの自由度(=6)
char JTYPE[k-th]：関節Jkのタイプ ’R’または’S’（‘RRRRRR’，’RRSRSR’など）
double AB[4][3]：ΣB→ΣAの座標変換行列
double As[k-th][4][3]：Σk →Σk-1への静座標変換行列(k=0,1,2,…,NFREE-1)
double As[NFREE][4][3]：Σn表示のワークの位置と姿勢
●戻し値 なし
●dynamics.cに作成する変数
NFREE：自由度
JTYPE[k-th]：関節タイプ
AB[4][3]：ΣB→ΣAの座標変換行列（一定）
AS[k-th][4][3]：静座標変換行列（As[k-th][4][3]と同じ）
WRKP0[3]：ワークのΣn表示の位置(As[NFREE][3-th)[3]と同じ）
WRKXN[3]，WRKYN[3],WRKZN[3]：ワークのΣn表示の姿勢（As[NFREE][0,1,2][3]と同じ）
（２－３）動的ロボットパラメータの受け渡し
setdynamics( rg, marm, Iarm )
●この関数に受け渡す変数
double rg[k-th][3]：アームL k の重心位置(m)（Σk 表示）
double m[k-th]：アームL kの質量(kg)
double Iarm[k-th][3][3]：アームＬkの重心回りの慣性行列(
)
●戻し値 なし
●dynamics.cに作成する変数
RG[k-th][3]：= rg[k-th][3]
MARM[k-th]：= m[k -th]
IARM[k-th][3][3]：= Iarm[k -th][3][3]
３．解析項目
（３－１）逆動力学
関節変位Φ，関節速度
，関節加速度
，外力／外モーメント
を与えて，
各関節部に加わる力FJk，モーメントMJk，関節に必要な駆動トルク（力）τを求める．
inv_dynamics( PHI, DPHI,
DDPHI, FEX, REXN, MEX, FJ, MJ, TJ )
●計算のために必要な既知変数（dynamics.cへ既に受け渡している変数．前準備による）
NFREE：自由度
As[k-th][4][3]：静座標変換行列
As[NFREE-th][4][3]：ワークの位置姿勢のΣn表示（n=NFREE-1）
m[k-th] ：アームL kの質量(kg)
rg[k-th][3]：アームL kの重心位置（Σk表示）(m)
Iarm[k-th][3][3]：アームL kの重心回りの慣性行列
()（Σk表示）
（k=NFREE-1のときはハンド・ワーク込みの質量・重心・慣性行列）
●関数への入力
double PHI[k]：Jk関節の変位φk( rad or m )
double DPHI[k]：Jk関節の速度
( rad/s or m/s )
double DDPHI[k]：Jk関節の加速度
( 
or 
)
double FEX[3]：外力（ΣA表示）(N)
double REXN[3]：外力のワーク上の作用位置（Σn表示）(m)
double MEX[3]：外モーメント（ΣA表示）（
）
●関数の出力
double FJ[k-th][3]：関節点J k に加わる力（Σk表示）(N)
double MJ[k-th][3]：関節点J k に加わるモーメント（Σk表示）(Nm)
double TJ[k-th]：関節J k に必要な駆動トルク（力）(Nm or N)
（３－２）動力学各項目の個別計算
の動力学式の，
（慣性項），
（コリオリ項），
（重力項）､
（外
力項）の各項を，関節変位
・速度を与えて求める．
dynamics_term( PHI, DPHI, FEX, REXN, MEX, INERTIA, CORIOLIS,
GRAVITY,
EXTORQUE, NMAX )
●計算のために必要な既知変数（dynamics.cへ既に受け渡している変数．前準備による）
NFREE：自由度
As[k-th][4][3]：静座標変換行列
As[NFREE-th][4][3]：ワークの位置姿勢のΣn表示（n=NFREE-1）
m[k-th] ：アームL kの質量(kg)
rg[k-th][3]：アームL kの重心位置（Σk表示）(m)
Iarm[k-th][3][3]：アームL kの重心回りの慣性行列
()（Σk表示）
（k=NFREE-1のときはハンド・ワーク込みの質量・重心・慣性行列）
●関数への入力
double PHI[k]：関節変位（rad or m）
double DPHI[k]：関節速度(rad/s or m/s)
double FEX[3]：外力（ΣA表示）(N)
double REXN[3]：外力のワーク上の作用位置（Σn表示）(m)
double MEX[3]：外モーメント（ΣA表示）（）
int NMAX：慣性項の次数（通常は=NFREE）
●関数の出力 （VW[], AW[]以外は全てΣk座標系表示）
double INERTIA[NMAX][NMAX]：慣性項(NFREE×NFREE)
double CORIOLIS[k -th]：関節J k に関するコリオリ項(Nm or N)
double GRAVITY[k-th]：関節J k に関する重力項(Nm or N)
double EXTORQUE[k-th]：関節J k に関する外力項(Nm or N)
（３－３）順動力学解析
の順動力学式において，関節変位Φ，関節速度を与えて関節加速度を求める．
direct_dynamics( PHI, DPHI, DDPHI, TJ, FEX, REXN, MEX )
●計算のために必要な既知変数（dynamics.cへ既に受け渡している変数．前準備による）
NFREE：自由度
As[k-th][4][3]：静座標変換行列
As[NFREE-th][4][3]：ワークの位置姿勢のΣn表示（n=NFREE-1）
m[k-th] ：アームL kの質量(kg)
rg[k-th][3]：アームL kの重心位置（Σk表示）(m)
Iarm[k-th][3][3]：アームL kの重心回りの慣性行列
()（Σk表示）
（k=NFREE-1のときはハンド・ワーク込みの質量・重心・慣性行列）
●関数への入力
double PHI[k]：関節変位（rad or m）
double DPHI[k]：関節速度(rad/s or m/s)
double FEX[3]：外力（ΣA表示）(N)
double REXN[3]：外力のワーク上の作用位置（Σn表示）(m)
double MEX[3]：外モーメント（ΣA表示）（）
●関数の出力
double DDPHI[k]：関節Jkの加速度( or )
（３－４）順動力学式の微分方程式の解（時系列）
の順動力学式を初期条件関節変位Φ0，初期関節速度0，関節駆動トルク（力）の時
系列
を与えて，時間関数
，
を求める．
dynamic_motion(
t0, dt, nf, PHI0, DPHI0, FEXSERIES, REXNSERIES,
MEXSERIES,
TJSERIES, PHISERIES,
●計算のために必要な既知変数（dynamics.cへ既に受け渡している変数．前準備による）
NFREE：自由度
As[k-th][4][3]：静座標変換行列
As[NFREE-th][4][3]：ワークの位置姿勢のΣn表示（n=NFREE-1）
m[k-th] ：アームL kの質量(kg)
rg[k-th][3]：アームL kの重心位置（Σk表示）(m)
Iarm[k-th][3][3]：アームL kの重心回りの慣性行列
()（Σk表示）
（k=NFREE-1のときはハンド・ワーク込みの質量・重心・慣性行列）
●関数への入力
double t0：運動の初期時間(s)
double dt：時間刻み(s)
int nf：時間刻みの数（tf=t0+nf*dt）
double PHI[k -th]：Jk関節の変位 ( rad or m )
double DPHI[k -th]：Jk関節の速度 ( rad/s or m/s )
double FEXSERIES[NF][3]：外力の時系列（ΣA表示）(N)
double REXNSERIES[NF][3]：外力作用点の時系列（Σn表示）(m)
double MEXSERIES[NF][3]：外モーメントの時系列（ΣA表示）(Nm)
double TJSERIES[NF][k-th]：Jk関節の駆動トルク（力）の時系列(Nm or N)
int NF ：時系列の次数(nf≦NF)
●関数の出力
double PHISERIES[NF][k-th]：Jk関節変位の時系列
(rad or m)
double DPHISERIES[NF][
k -th]：Jk関節速度の時系列
(rad/s or m/s)
４ ．使用の注意
（１）運動学の関数を使う前にEtoA( )またはsetrobot( )の予備計算を行う（座標変換行列を決めるため）．
１度これを計算すれば，ロボット構造・ワークの位置姿勢が変わらない限り，その
後運動学の関数を何回でも使える．
（２）extern int
analys_vel_acck( );
extern int inv_dynamics(
);
extern int dynamics_term( );
extern int direct_dynamics( );
extern int dynamic_motion( );
extern int EtoA( ); (または setrobot( ); )
を定義する．
（３）ベクトルの配列は[0],[1],[2]，…，マトリクス[3][3]の成分は第１行 ([0][0] [1][0]
[2][0])，第２行([0][1] [1][1] [2][1])，第３行([0][2] [1][2] [2][2]) の順で
ある．
（４） 関節J0 の変位はPHI[0]，J1 の関節変位はPHI[1]，J2 の変位はPHI[2]，．．．で
ある．
（５）E[3][3] = (ex, ey, ez)は，E[0-th][3] = ex, E[1st][3] = ey, E[2nd][3] = ezである．
［参考］
使用例はdtest.cを参照のこと．
［参考文献］
「詳説ロボットの運動学」，高野政晴，オーム社，2004．