３．１０．３　薄壁の円形穴を通り抜けて位置決めする運動解説　　　　　２０１２−０６−１０

（実行ファイル3-10-3ThinHolePassexe）

「詳説ロボットの運動」第８章８.２.5項参照）

［3-10-3ThinHolePass(12-6-10)に含まれるフォルダ・ファイル］

・シミュレータ：フォルダ名 ThinHolePass

・解説のファイル

・本解説：3-10-30ThinHolePassManual:

・補足説明　3-10-3ThinHolePassCom

１：干渉回避しながらゴールポーズから初期ポーズへの経路逆生成−局所的衝突回避法−

3-10-31ThinHolePassGeneration

２：経路生成におけるJMの旋回円上の特徴点：3-10-32JMCirclePnt

３：壁内外で単位ベクトルを壁床から遠ざける回転運動：3-10-33WFApartMotion

４：ワーク（RP関節の先の関節）の目標を干渉しない方向に修正：3-10-34WorkDirRevise

５：ロボットアームの自己干渉の検証：3-10-35SelfCollision

６：薄壁穴にアームを通す２関節角を求める逆運動学：3-10-36 ThinHoleInverseNew

目次：

［シミュレーションにおける前提］　　　　　　　　　　　　　　　　　　　　　　　　　　1p

［シミュレータの使い方］  1p

［壁床干渉を避けながら経路逆生成する方策］ 5p

［薄壁穴通り抜け位置決め問題の特徴］ 6p

［「局所的干渉回避法」で使う幾つかの計算］ 6p

・薄壁の円形穴を通り抜けてワークを目標位置へ位置決めすることと，初期ポーズからゴールポーズまでの経路生成問題である．

・薄い壁なので通り抜けた先で上下左右にアームを回してかなり自由に動かすことができ，壁際でも位置決めすることができる．

・穴を通り抜けかつ目標に位置決めを同時に満足する解法がないので，最終解は穴通り抜け（‘b’）と目標に位置決めする逆運動学（’a’）との繰り返し演算で求める（第８章８.２.5項）．

・このシミュレータでは，初めに穴を通り抜けかつ目標に位置決めする最終解を繰り返し演算で求め，次に最終解のポーズ（関節変位qG）から初期ポーズ（関節変位q0=0）まで穴を通り抜ける経路を逆生成する（別紙参照）．生成後に経路追従の運動シミュレーションを行う．

［シミュレーションにおける前提］

・ロボットタイプ：

８自由度ロボット４×２種（(1-1).RPP,  (1-2)RQP,  (1-3)PQQ,  (1-4)PRP,  (2-1)RP,  (2-2)QP, 及びリストRPR）

についてシミュレーションする．（P,Q,RはX,Y,Z軸を回転軸とする関節．直動関節は扱わない．オフセットなし）

・関節角の制限

　隣同士のアームが喰い込むことを避けるために，P,Q関節に角度の制限を設ける． R関節の制限はない．

・穴通り抜け・位置決めする関節

　穴を通り抜けるために必要な関節は２つ(L)，位置決めする関節は３つ(I, J, K)である．姿勢決めを含めて８自由度が必要である．

穴を通り過ぎる運動ができるためには穴通り抜けの前の関節は３以上必要である．２関節だと穴を通るアームは存在するが動けない．

　リストの関節( 6, 7,8)=(RPR)は姿勢決めをする．これは変更しない．

・ロボットの位置・諸元

　ロボットベースは静止座標系の原点とする．ロボットタイプが変わってもアーム長・太さなどは変えない．

・障害物（薄壁，穴）

薄壁穴中心位置を，壁面の法線ベクトルをとする．穴はロボットアーム・関節部が斜めになっても通り抜けられる程度の直径で空いているとする．

穴の位置は変えられる．

・ワークの目標位置姿勢

　ワークの目標は床上に置かれるとし，その位置は(X,Y)方向に変えられる．

　姿勢は直方体ワークを上から下向きに置くとする．変更しない．

［シミュレータの使い方］（シミュレータのフォルダ名：ThinHolePass）

（１）フォルダ内使用ファイル

・program名：ThinHolePass.c, THINHOLE.c, POINV2.c, funcall.c, graph3d.c

（２）文字画面でのキー操作

・設定変更やシミュレーションは全て描画画面で操作する．

・計算の節目に計算結果が印刷されるので，必要があれば見ればよい．

（３）描画画面におけるキー操作

・パラメータ変更の操作（キー操作）

　‘F’：ロボット選択モード → ４×２種から11, 12, 〜41, 42のどれかをキーインして選択 → 画面がＡモードへ変わって選択したロボット表示

　‘O’：障害物設定モード：(1,4)，(2,5)，(3,6)キーで穴中心位置を±(X,Y,Z)方向へ移動 → ‘A’キーでＡモードへ

→ 描画画面へ

　‘A’：（１）ワークの目標位置変更モード：ワークの目標位置を(1,4)，(2,5)，(3,6)キーで±(X,Y,Z)方向へ移動

（２）ロボットの最終目標ポーズ計算モード：穴を通り抜けて位置決めする最終解を得る計算

（２−１）SPキー：計算前に繰り返し計算の候補となる初期ポーズが複数表示されるので１つを選択

（２−２） ‘a’：位置決め計算 → ‘b’：隙間通り抜け計算 → この繰り返し（’a’,または’b’だけの繰り返しも可）

　‘B’：経路生成モード：最終解のポーズから初期ポーズに到る経路を逆に求める計算：’s’により自動的に進む．

　‘C’：軌道上の運動モード → ‘s’キーで初期ポーズから目標に到るポーズへの運動描画

　ESC：終了

［註１］’A’の計算で，’a’によってワーク目標への位置決めの解を得るが穴を通り抜ける保証はない．同様に’b’によって穴を通り抜けても目標に位置決めできるとは限らない．’a’,’b’の繰り返しによって通り抜けと位置決めの両方を満足する解に収束する．

［註２］’A’の計算で，’a’のよって位置決めの解を得てもその解に急には変えず，少しづつ進めるようにしている．’b’も同様である．そうでないと最終解に収束しない恐れがある．’a’または’b’だけを続けてもよい．

・画面表示の操作

　‘s’：時間経過による経路逆生成・運動の推移

 ‘x’, ‘X’,  ’y’, ‘Y’,  ‘z’,’Z’：Ｘ, Y, Z座標を正負に移動

‘p’, ‘P’,  ‘q’,’Q’,  ‘r’,’R’：X,Ｙ,Z軸回りに正逆に回転

　‘0’：軌道上の運動を初期状態に戻す

［註１］ロボットタイプ・目標位置・壁（穴）位置等は仮に設定されている．

［註２］設定変更はどの時点でもできる．但し前の情報は失われる．

［シミュレーションの例］

・図１，図２：始めの表示とロボット選択，目標位置変更

　‘F’：ロボットの選択

’O’：薄壁の穴中心位置変更：(1,4),  (2,5),  (3,6)キーにより±(X,Y,Z)方向へ移動

目標位置はこのＡ内で(1,4),  (2,5)キーにより±(X,Y)方向へ移動

　ここでは予めロボット・目標位置・穴位置を設定しているので変更があれば上記の操作をする．

壁はY軸正の方向（図の右側）にあることが望ましい．

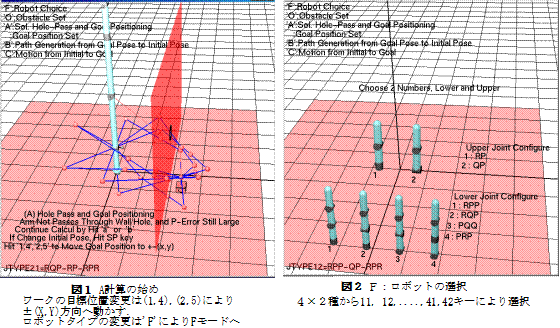
・図３，図４：Ａ計算のワーク目標への位置決め(Aa)と穴通り抜け(Ab)の繰り返し計算とその初期ポーズ

　SPキーによる初期ポーズの選択

　‘a’，’b’キーによって(Aa)計算と(Ab)計算の繰り返し

［註１］初期ポーズによって最終解が異なることも同じこともある．また解が収束しないこともある．

［註２］‘a’，’b’の交互でも続けて’a’，’b’でも構わない．繰り返しの仕方によっては異なる最終解に到達する場合もあり，また本来解があるのに解なしの結果となる場合もある．

　途中で’A’キーを押せば始点に戻りやり直しができる．

　

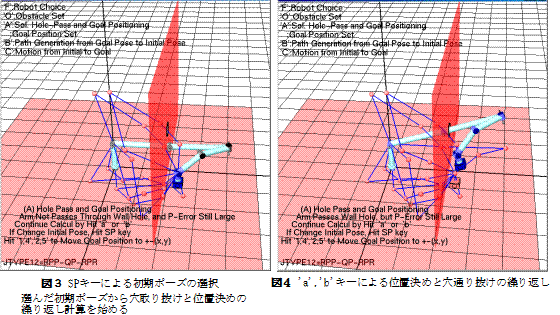
図４，図５：A計算終了とB計算へ移行

　繰り返し解が十分収束すると画面に「**Final Solution …….. Obtained 」が表示され，Bモードへの移行が可能となる．

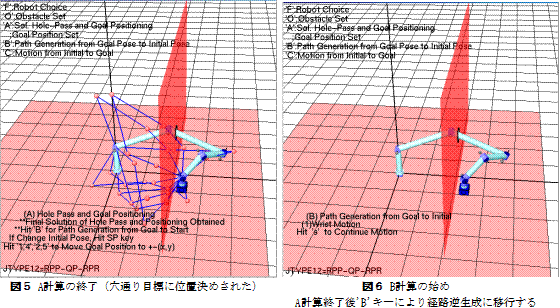
図７〜図１１：B計算

　‘s’キーにより１ステップづつ経路の逆生成が進む．

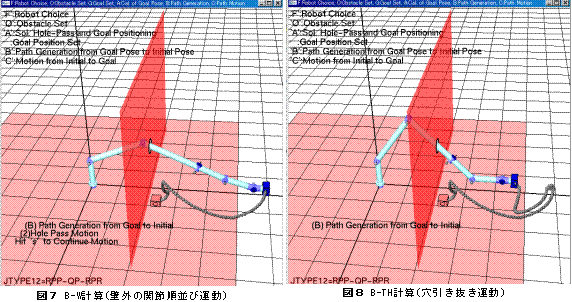
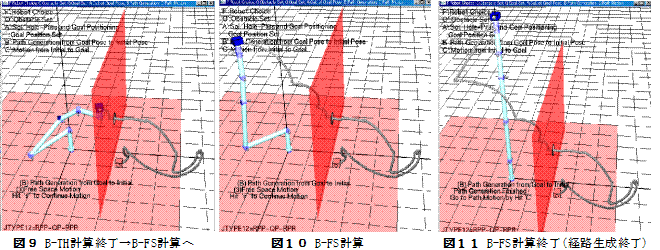
図１２：経路生成後の初期ポーズから目標までの経路追従運動

　‘s’キーにより１ステップづつ進む．

図１３〜図１５：経路生成中に干渉回避できず，経路生成不能となった例

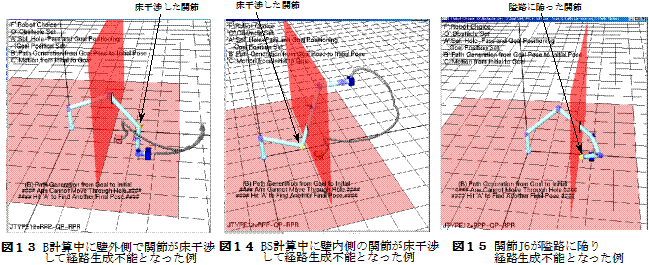
［薄壁穴通り抜け位置決め問題の特徴］

１．ロボットタイプによる最終位置決めの難易

・ロボットは８自由度でその関節は全て回転関節としたが，直動関節は８自由度では位置決めできる領域が狭い．

・Ｚ軸回りの関節軸をＲ，Ｘ，Ｙ軸の関節をＰ，Ｑと名付ける．

・根元の関節J1=Rのロボット（ロボットタイプ１，２）は穴通り抜けて位置決めできる領域が広い．J1=P, Qのタイプ３，４は領域が狭い．

・中間にＲ関節を持つタイプは先の方のアームを比較的自由にどの方向へも伸ばせるので，最終解を得るのに有利である．

・しかし，Ｒ関節を含むアームが長いので（ロボットはどのタイプも全長を等しくしている），壁穴位置がロボットベースに近いとアームを穴から引き抜くのが難しくなる．

・壁の向こう側で手が届く限り位置決めできるようにするには，壁の向こうに６自由度が欲しい．すなわちこの問題には９自由度以上が操作上望ましい．

２．経路生成

・初期ポーズは全ての関節変位q=0とする．

・経路生成にはリスト角=0とする運動と壁外側で関節を順並びとする運動（Ｗ），通り抜け運動（TＨ），自由空間運動（FＳ）に分けた．

・(W)ではリスト角だけでなく，壁からアームを引き抜く前に壁の向こう側の関節角も0へ近づけ，壁に衝突することを避けている（後述・別紙）．

・(TＨ)でも壁の向こう側の関節角を同様に理由で0に近づけている．

・壁通り抜け後，(FＳ)の自由空間運動は，壁床と衝突することを避ける運動を生成している（後述・別紙）．

・更に(FS)でワークが初期位置の近傍(Ｃに来たら，全ての関節変位qを0に近づける．これがないと初期ポーズが同じでq=0でない別の値になる可能性がある．

・滑らかでできるだけ短い経路が最良の経路であり，人間は無意識に最良経路を選択している．

・人間の動作を模倣して最良の経路を生成するにはアーム・ワークと壁の位置関係を把握しながら逐次経路点を決定する高度な知能行動が必要であろう．

［薄壁穴にアームを通す２関節角を求める逆運動学］：ファイル名A.ThinHoleInverseNew参照

・ここでは「詳説ロボットの運動学」８．２．５項に述べた計算法と違う方法を採用している．

・８．２．５項ではアームＭを穴に通す２関節をq[L], q[M]としているが，もっと一般的にq[L],q[m]の２関節により通す問題を定式化している．

［壁床干渉を避けながら経路逆生成する方策］

・経路の生成は穴通り抜けて目標に位置決めされた状態（ゴールポーズ）から初期状態（初期ポーズ）へと逆に生成する．正の経路生成よりこの方が運動の制約が少ないからである．

・壁外側でアームが壁を通り抜けるためにはアームが壁から外側に伸びた状態（関節角q[]=0）とするのが望ましいが，無条件に伸ばせば壁床または自己干渉する可能性がある．

・壁穴からワークを含めて全て引き抜いた後に初期ポーズへ到る経路逆生成においても，無条件に伸ばせば同様に干渉の可能性がある．

・それを避けるために「局所的干渉回避法」を採用する．

・これは１つの関節JMを伸ばすときに，次の関節JMH（アーム）が干渉しない運動ができるかどうかを考慮してその目標を決める方法である．

・以下の方策の詳細は別紙に述べる．

（１）経路逆生成（「干渉回避しながらゴールポーズから初期ポーズへの経路逆生成−局所的衝突回避法−」：ファイル名1ThinHolePassGeneration参照

・逆生成は次の３経路逆生成からなる．

（１−１）ＢＷＲ：ゴールポーズから壁外側でアームを伸ばした状態（関節の順並び）までの運動

・伸ばしきれないで行き詰まった状態になったらそのままで（１−２）ＢＴＨへ移る．

（１−２）ＢＴＨ：壁外側の干渉回避しながらアームを穴から引き抜く運動（上記参照）

・全ての関節・ワークが通り抜けるまで続ける．

・ここでも行き詰まったら経路逆生成できないことを意味する．

（１−３）ＢＦＳ：関節・ワークの全てが壁内側に来た状態から初期ポーズまでの運動

［「局所的干渉回避法」で使う幾つかの計算］

（１）「JMの旋回円上の特徴点」：ファイル名2JMCirclePnt参照

・経路逆生成における関節JMの目標点計算

・「局所的干渉回避法」では関節JMは関節JMFを中心にq[MF]によって旋回し，その旋回円上に目標点を定める．

（２）「壁内外で単位ベクトルを壁床から遠ざける回転運動」：ファイル名3WFApartMotion参照

・JMの前２つの関節JME, JMFがRPの場合は，q[ME], q[ME]によってJMを任意の方向へ向けることができる．

・すなわちアームを伸ばす方向へ壁床と干渉しないように持っていくことができる．

・この方向とそこに到る壁床から遠ざかるような方向ベクトルの運動を求め，その方向ベクトルを与える関節角q[ME], q[ME]を求める（姿勢逆運動学）．

（３）「ワーク（RP関節野崎の関節）の目標方向を干渉しない方向に修正」：ファイル名4WorkDirRevise参照

・JMFが低すぎると目標のアームを伸ばす方向では関節JMが床と干渉する場合がある．また，その方向を与えるq[MF]が限界を超える（前のアームに喰い込む）場合がある．

・これらの場合の目標方向を修正する計算法を示す．

（４）「ロボットアームの自己干渉の検証の計算」ファイル名5SelfCollision参照

・各アーム間の距離（アーム間最短距離，関節間距離等）を計算し，余裕値以下を自己干渉とする．

・隣のアーム間は，その間の関節角が限界値以上の場合を自己干渉とする．