３．１１．２１ PR接触によるワークの操りシミュレーションの説明書　 2023-1-17

ソースファイル：FinPRManip1Source.zip　　実行ファイル：FinPRManip1exe.zip

PR運動別解法： PRMotionCacul

FingarManip.c, FingerGraspKine.h, PRManip2.h, FinKine2.h, FinFUNCALLx.h

Fingraph3d.h, FinGraph3d2.h, defineVar1.h, glut32.dll

PR運動の別解法：PRMOtionCalcul

・PR接触は人の指のようにワークとの間に大きな摩擦力があり，相対的な滑りもツイストもない純転がり運動をする接触状態のことである．

・滑り・ツイストがある接触では運動が不確実となる可能性があり，それに対してPR接触は指とワークの運動は力学に関係なく運動だけで決まる確定的な運動であり，操りに向いている．

・指の腹によるPR操り運動に限定する．指先による操りは別シミュレーターで扱う．

・円筒の操りは円筒面接触に限定する．円筒の端面やその円環で接触する操りは別シミュレータで扱う．

シミュレーターの使用法

Hand と Work

・全て描画画面上でkeyにより実行項目の選択や条件設定ができるようになっている．

・用意されたHand とWork

　Hand：指数nF=2 or 3

関節数nJ=4 ，PR運動に必要な数

関節構成 RQPP, PQPP(人指の構成)0

Work：球，有限円筒

シミュレーターの実行操作

［条件設定のkey操作］

(W) Workの選択 : ‘W’ → ‘1’ :球，or ‘2’ :円筒

(H) Handの選択：’H’ → ‘1’ :2F×RQPP, ‘2’ :3F×RQPP

‘3’ :2F×PQPP, ‘4’ :3F×PQPP

(M) Workの位置姿勢の変更：’M’ → ’X’ ,’x’, ‘Y’, ‘y’, ‘Z’, ‘z’　： X,Y,Z方向に1step座標移動

　　　　　　　　　　　　　　 ’P’ ,’p’, ‘Q-’, ‘q’, ‘R’, r’ ： X,Y,Z回りに1step回転

　(J) 指関節角の初期値変更：’J’ → ’n’ (指番号), ‘m’ (関節番号), ‘p’ or ‘m’ 角度の増減

(V) Work運動の速度角速度の変更：’V’ → ‘X’, ‘x’, ‘Y’, ‘y’, ‘Z’, ‘z’ ; 各方向の速度増減

　　　　　　　　　　　　　　　　　　 ‘P’, ‘p’, ‘Q’, ‘q’, ‘R’, ‘r’ ; 各方向の角速度増減

　(I) 座標系の変更（視点の変更）：’I’ → ‘X’, ‘x’, ‘Y’, ‘y’, ‘Z’, ‘z’ ; 各方向へ座標1step移動

　　　　　　　　　　　　　　 ‘P’, ‘p’, ‘Q’, ‘q’, ‘R’, ‘r’ ; 各方向へ角速度1step増減

［計算実行のkey操作］

(G) Workの把握計算：’G’ → ‘s’ : 指番号1,2,3の順に計算

(A) PR接触による操り運動計算：’A’ → ‘s’:微小時間dt毎のPR運動

(D) 操り運動の再現：’D’ → ‘s’: A運動の再現

PR操り運動の例

・最初の画面

Hand1=1 : 2Fin×RQPP

Work1=1 : 球

Workの速度角速度

vw[ ]=(0,0,0), ωw[ ]=(0.02, 0, 0)

本progamではこの設定で始まる．

条件変更があればここで行う．

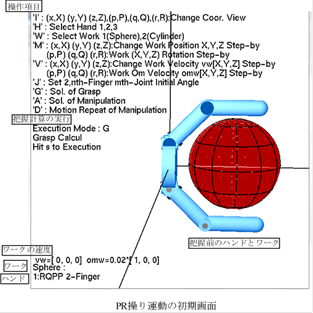
・把握計算：‘G’ Mode

key=’G’ →’s’ → ‘s’

　(初期画面では既に’G’となっている)

　key=’s’ : 1指毎に把握結果表示

　[註1] 把握の解がないときはその表示が出る．

　　　　別条件で再計算したいときは操作項目から

　　　 選んで最設定する．

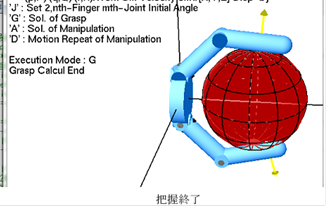
・操り計算：‘A’ Mode

　key=’A’ → ‘s’

‘s’で1stepずつ進む．(全ての指のPR操り運動を1step進める)

　各stepでWorkとhandとの干渉が生じたとき，PR接触が行き詰まったときはその時点でA計算は停止する．

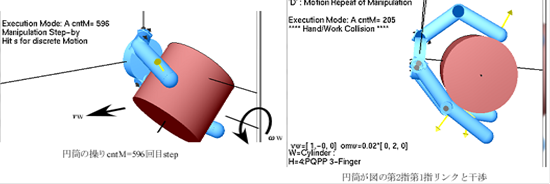
・操り運動の再生：’D’ Mode

key=’D’ → ‘s’

A計算の結果を再現する．指・Work上の

接触点がどのように動くかがよく分かる．

　

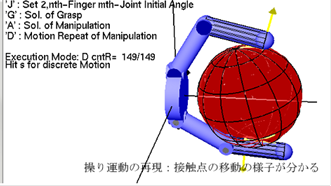
・条件変更

　操作項目から選んで以下のkey操作をする．

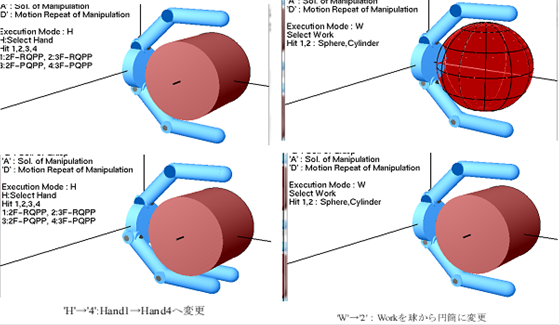
　Handの変更

key=’H’ →’1’ or ‘2’ or ‘3’ or ‘4’

‘1’ : 2指×RQPP

‘2’ : 3指×RQPP

‘3’ : 2指×PQPP (人の指型)

‘4’ : 3指×PQPP (人の指型)

Workの変更

key=’W’ → ‘1’ or ‘2’

‘1’ : 球

‘2’ : 有限円筒

　Workの位置姿勢変更

key=’M’ → ‘X’, ‘x’ ‘Y’, ’y’, ‘Z’, ‘z’

(±X, ±Y, ±Z)方向へ1step移動

→ ‘P’, ‘p’ ‘Q’, ’q’, ‘R’, ‘r’

(X, Y, Z)軸回りの±1step回転

　初期関節角の変更

key=’J’ → ‘nF’ → ‘nJ’ → ‘p’ or ‘m’　の順に入力

nF :指番号，nJ : 関節番号，p, m : 関節角増減

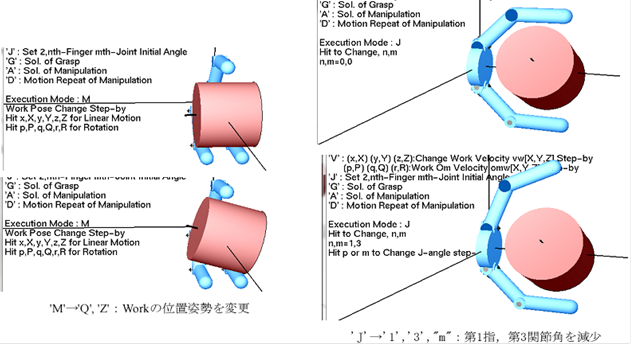
Work速度の変更

‘V’ → ‘X’, ‘x’, ‘Y, ‘y’, ‘Z’, ‘z’ ：vw[x,y,z](mm/s)を増減

→ ‘P’, ‘p’, ‘Q’, ‘q’, ‘R’, ‘r’：omw[x,y,z](rad/s)を増減」

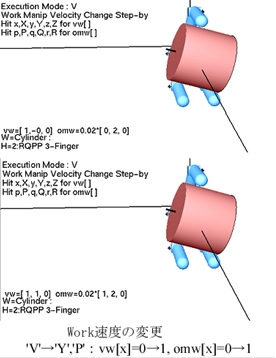
［PR接触による操りの結果の考察］

・指関節構成を RQPPとPQPPの2種を取り上げた．

　前者は可動範囲が広くまた接触する指の姿勢変化も広い．後者は人の指関節構成と同じであり一般的に接触指の姿勢変化に制限がある．

　PR操りにとって後者はすぐに行き詰まるだろうと予想していたが，結果は前者と変わりがなく，Workが掌や操る指以外の指に干渉するまでは行き詰まりはない．行き詰まりとは，接触点CからPR条件によって決まる必要関節速度の解がない，すなわち特異点に陥るということである．PRPP構成も作業領域内で特異点があるのは希だということである．

　PQPP構成指の特異点は，q1=q2=0で接触点がq3, q4の回転面(Y, Z)平面内にありWorkの回転運動がY軸回りという場合が１つの例である．この状態で指はY軸回りの回転ができないからである．

　多くのtrialを経なければ確実なことは言えないが，RQPPでなくてもPQPPの人型指関節構成でPR運動に差し支えないようである．

・操りが不能となるのは指ポーズが大きく変わり指上の接触点が移動して指の円筒面から外れる場合である．これはワークの大きくない移動回転量で生じる．

　例えば球を1回転させる操りには持ち替えが必要である．これは人の指の操りにもよく見られることである．

PR運動の解法　　　　　　　 　　　　　　　　　　　　　　　　2023-1-17

PRManip.h PRMotion1( ), PRSphMotion24( ), PRCylMotion24( );

・円筒指がワークと接触してPR運動する解法を考える．

・「詳説ロボットの運動学 9.4.1 指の腹による物体操りの接触運動特性」の(a) PR接触運動条件は

　ワークと指野原の接触点Cにおける速度と回転速度をvwc[ ], vfc[ ], ωwc[ ], ωfc[ ]とすると

vfc[ ] = vwc[ ], (ωfc[ ], nc[ ]) = (ωwc[ ], nc[ ])

であり，この4条件を満足する指の4関節の変位速度ν[ ]が確定する．

　微小時間dt後の関節角は

dq[ ] = ν[ ]*dt, q2[ ] = q1[ ] + dq[ ]

この関節角から指のポーズが決まり，新しい接触点が決まる．

・この計算はC点の移動がdt時間の直線運動であり，dtを十分に小さい値にしなければ誤差が生じ，長い時間でその誤差が累積して正しい運動と異なってしまう．（非ホロノーム系の特徴）

　指とワークのPR接触運動では上記dt後に接触がわずかに離れる．

第2PR運動

・PR運動を以下のように変形する．dt後の状態

(1) 指とワークは接触する．or 指面とワーク面の最短距離D = 0

(2) 指とワークの転がり量は等しい．Sf = Sw

(3) dt後の転がり軌跡sf[ ], sw[ ]の接触平面内の方向ベクトルは等しい．

(4) 指とワークの接触点における回転速度の法線方向成分は等しい. ωfcn = ωwcn

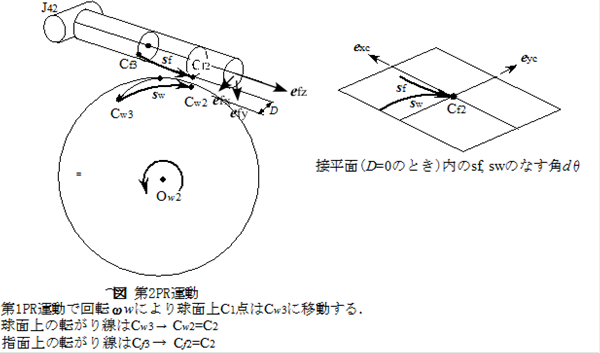
これらを数式で表現すると以下のようになる．

・指の初期関節角q1[ ], 接触指（第4指）の関節位置J41[ ], 接触点位置rfc1[ ], 接触点までのリンク長Lf1, 指円筒回りの偏角φf1

rfc1[ ] = J41[ ] + Lf1*efz1[ ] + af*(exf1[ ]*cos(φf1) + eyf1[ ]*sin(φf1) )

・ワークの初期位置rw1[ ], ワークの接触点位置rwc1[ ]

球面の場合：接触点のparameter αw1, βw1

rwc1[ ] = rw1[ ] + aw*(cos(αw1)*sin((βw1) + sin(αw1)*sin(βw1) + cos(βw1) )

円筒面の場合：接触点のparameter Lf1, φf1

rwc1[ ] = rw1[ ] + Lw1*ezw1[ ] + aw*(exw1[ ]*cos(φw1) + eyw1[ ]*sin(φw1) )

・ワークの代表点の速度vw[ ], 代表点回りの回転速度ωw[ ]

・dt後のワークの位置rw2[ ], 接触点の移動先rwc3[ ]

rw2[ ] = rw1[ ] * vw[ ]*dt

rwc3[ ] = rw2[ ] + ωw[ ]×(rwc1[ ] – rw1[ ])

・dt後の指の関節変位の増分dq[ ], 関節角q2[ ], 折衝\句点の移動先rfc3[ ]

　q2[ ]を与えると指の諸元が決まる．

q2[ ] = q1[ ] + dq[ ]

rfc3[ ] = J42[ ] + Lf1*ezf2[ ] * af*(exf2[ ]*cos(φf1) + eyf2[ ]*sin(φf1))

・dt後の指-ワーク間の最近点Cf2, Cw2位置rfc2[ ], rwc2[ ], そのときの指parameter Lf2, φf2

rfc2[ ] = J42[ ] + Lf2*ezf2[ ] + af*(exf2[ ]*cos(φf2) + eyf2[ ]*sin(φf2))

球面の場合のparameter αw2, βw2

rwc2[ ] = rw2[ ] + aw*(cos(αw2)*sin((βw2) + sin(αw2)*sin(βw2) + cos(βw2) )

円筒面の場合のparameter Lw2, φw2

rwc2[ ] = rw2[ ] + Lw2*ezw2[ ] + aw*(exw2[ ]*cos(φw2) + eyw2[ ]*sin(φw2) )

・第2PR運動の誤差は上記の諸元から求められる．

(1) 指-ワーク間の最短距離D

D = abs(rfc2[ ] – rwc2[ ])

(2) 指・ワークの転がり量の差 dS

sf[ ] = rfc2[ ] – rfc3[ ], Sf = abs(sf[ ])

sw[ ] = rwc2[ ] – rwc3[ ] Sw = abs(sw[ ])

dS = Sf – Sw

(3) 指・ワークの接平面内の転がりベクトルesf[ ], ews[ ]のなす角dθ

接平面内のベクトルexs[ ], eys[ ]：exs[ ] = ezf2[ ], eys[ ] = exf2[ ]とする．

efs[x] = (sf[ ], exs[ ]), sfs[y] = (sf[ ], eys[ ]), θf = atan2(efs[y], efs[x])

ews[x] = (sw[ ], exs[ ]), sws[y] = (sw[ ], eys[ ]), θw = atan2(ews[y], ews[x])

dθ = θf – θw

(4) 接触点C2における指とワークの回転速度の法線方向nc2[ ]成分ωfn, ωwn

関節速度 ν[ ] = dq[ ] / dt，関節軸ベクトル AX[ ]

ωf[ ] = AX[1]*ν[1] + AX[2]*ν[2] + AX[3]*ν[3] + AX[4]*ν[4]

ωfn = (ωf[ ], nc2[ ])

AXN[ ] = (AX[ ],nc2[ ])と置くと

ωfn = AXN[1]*ν[1] + AXN[2]*ν[2] + AXN[3]*ν[3] + AXN[4]*ν[4]

ωwn = (ωw[ ], nc2[ ])

dωn = ωfn – ωwn

・誤差 ERR[ ] = (D, dS, dθ, dωn)を0とするdq[ ]をNewton法によって求める．

　　 ERR[ ] = JB4[ ][ ] * dq[ ]

dq[ ] = IJB4[ ][ ]*ERR[ ]

q2[ ] = q1q[ ] – dq[ ]

・特異点では運動が行き詰まる．

det = |JB4[][]| = 0