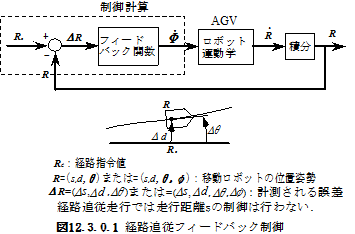
１２．３．０　経路追従フィードバック制御の基本                 　２００８−１０−２

実行フォルダ  AGVFBC0exe

 

・誤差フィードバックによる経路制御の基本形を論じる．

・移動ロボットの制御系は本質的に非線形であり，線形化して系を考えたとき，誤差が大きいと線形系とは異なる挙動を示す．どのように違って来るかを知ることがこのシミュレーションの目的である．

・どの場合も「経路制御(Path control)」とし，経路からのずれΔd，傾きの誤差Δθを旋回（またはステアリング）にフィードバックすることとする．

・AGVは経路を知っているとする．すなわち経路の曲率κによって決まるステアリング角φcを知っており，ステアリング角誤差をフィードバックすることができる（2DW1C機構では必要ない）．

・AGVの駆動輪速度は2DW1C・1RDW1FS機構では一定とする．1FDW1FS機構では経路曲率の急変化に着いていけるように速度を下げる．この速度の変化は経路が分かっているので駆動輪速度指令値vdとして予め決めでおくことができる．

・フィードバック制御の基本は，経路からのずれΔdとAGVの経路に対する傾きのずれΔθ，及びステアリング(ST)付きのAGVではST角のずれΔφの誤差をフィードバックする単純制御(P制御)と積分要素を加えたPI制御である．

・P制御とPI制御の制御性の違いを即応性・定常誤差・安定領域の広さなどで調べる．

［註］ 経路からのずれΔdの取り方には２通りある．１つはAGVが計測するとしてAGVから真横に見た経路までの距離，もう１つは経路から直角方向に見たAGV位置までの距離である．前者はAGVの向きによって経路を見失うことがあり，制御はこの時点で経路追従失敗として終わる．後者は経路が閉曲線か無限曲線（直線）であればΔdは必ず存在する．

　このシミュレーションでは後者のΔdを採用する．

 

［目次］

１．単純P制御とそのフィードバックゲイン

（１）2DW1C機構の単純P制御のゲイン

（２）1FDW1FS機構の単純P制御のゲイン

（３）1RDW1FS機構の単純P制御のゲイン

２．PI制御とそのフィードバックゲイン

（１）2DW1C機構のPI制御のゲイン

（２）1FDW1FS機構のPI制御のゲイン

（３）1RDW1FS機構のPI制御のゲイン

３．経路追従制御のソフトウエアサーボ

［シミュレーションの使い方］

［AGV経路誤差フィードバック制御の特徴］

 

 

・経路をまたはで表す．経路指令値はまたは，誤差はまたはである．

・AGVの制御変数は駆動輪速度と旋回速度，または駆動輪速度とST速度である．

・経路追従制御では走行距離sの制御は行わない．走行速度（駆動輪速度）は指令値のみに従い，経路誤差Δsのフィードバックは行わない．

・駆動輪速度はvd =一定とし，フィードバック制御は行わない．

・ここでは経路追従制御を取り上げ，経路上の距離の誤差Δsは無視する．

・従ってまたは，または，またはとして追従制御を論じる．

・系の一般的な式は以下の通りである．

・フィードバック関数・AGVの運動学・積分を併せ，その一巡伝達関数をG(s)とする．

・指令値Rcに対する応答Rは

　　　　　　　　　　　　　　　　　　　(0-1)

・誤差の指令値に対する伝達関数は

　　　　　　　　　　　　　　　　　　　　(0-2)

・G(s)，1+G(s)は行列である．しかし今後の具体的な計算では，行列の形では却って煩わしいので，１変数として論じる．

 

 

１．単純P制御とそのフィードバックゲイン

 

（１）2DW1C機構の単純P制御のゲイン

 

・２駆動輪速度でなく，換算して走行速度と旋回速度について考える．

　　　                                               (1-1-1)

　　　                                              (1-1-2)

・誤差を旋回速度にフィードバックする．

　　　                                        (1-1-3)

・走行速度はこのAGVでは一定速度でよい（どんな急旋回でもできる）．

・フィードバックを含むAGVの運動方程式と，誤差が小さいとしてその線形化式は

　　　                     　                   (1-1-4)

　　　                 　                 (1-1-5)

・Laplace変換して

　　　                                       (1-1-6)

　　　，　　                     (1-1-7)

・Δθについてまとめると

　　　　　　　　　　　　　　　　　　　　(1-1-8)

・前記のG(s)は

                                       　(1-1-9)

である．

・特性方程式は

　　　                                             (1-1-10)

・系の特性を

　　　                                             (1-1-11)

とするFBゲインは

　　，　                                      (1-1-12)

である．

 

（２）1FDW1FS機構の単純P制御のゲイン

 

・目標経路は分かっているとする．駆動輪速度vdは一定とし，誤差フィードバックは行わない．

・誤差は経路ずれとステアリング(ST)角誤差であり，ST速度ωにフィードバックする．

　ST角誤差は，経路が既知であるからどの地点で指令のST角φcが分かっており，である．

・誤差をステアリング(ST)速度にフィードバックする．

　　　，　                (1-2-1)

・駆動輪速度vdは一定とする．

・AGVの運動方程式は

　　　                                    (1-2-2)

　　　，　，　　　(1-2-3)

・誤差が小さいとして系を線形化する(Lはトレッド)．また指令の走行速度は

　　　                                             (1-2-4)

　である．誤差の式はラプラス変換して

　　　                    　　 (1-2-5)

，　　　          　　 (1-2-6)

　　　　　　　　              (1-2-7)

・Δφについてまとめると

      　　　  　　　　　　　 (1-2-8)

・前記のG(s)は

                              (1-2-9)

　（この形はサンプル値制御に利用する）

・特性方程式は

　　　                        (1-2-10)

・系の特性を

　　　　→　   (1-2-11)

　となるようにゲインを決める．

　　　，　，　         (1-2-12)

　　　， 　                                                     (1-2-13)

・であるから，ST角φcによってゲインは異なり，のときゲインはφc=0のときより大きい．仮にφc=0としてゲインを決め一定に保つとすると，のときにはゲインは小さめに設定したことになり，これは応答性は悪くなるが安全側である．

 

（３）1RDW1FS機構の単純P制御のゲイン

 

・1FDW1FS機構と同様に，誤差は経路ずれとステアリング(ST)角誤差であり，それらの誤差をステアリング(ST)速度にフィードバックする．

　　　，　　 　          (1-3-1)

・駆動輪速度vdは一定とする．

　　　                                                      (1-3-2)

・AGVの運動方程式は

　　　                                          (1-3-3)

　　　，　，　   (1-3-4)

・誤差が小さいとして系を線形化し，Laplace変換する(Lはトレッド)．

　　　                                              (1-3-5)

                  　　               (1-3-6)

　　　                        (1-3-7)

・と置き換える．                                        (1-3-8)

・Δφに関する式は1FDW1FSと同じ形をしている．

       　　　　       　　　　 (1-3-9)

・前記のG(s)は

                                (1-3-10)

　（この形はサンプル値制御に利用する）

・特性方程式は

　　　                          (1-3-11)

・系の特性を

　　　　→　   (1-3-12)

　となるようにゲインを決める．

　　　，　，　          (1-3-13)

　　　， 　                                                      (1-3-14)

・vsは通常は一定であるが曲率の急変化の部分では小さくするすなわち可変である．．であるからφcによって変わる．φc=0のゲインに固定するとφc≠0のときはゲインを大きく設定したことになり，これはωnとζを設定より大きくする．線形理論では安定ではあるが，AGV運動の非線形性のために不安定になる可能性がある．

 

２．PI制御とそのフィードバックゲイン

 

（１）2DW1C機構のPI制御のゲイン

 

・２駆動輪速度でなく，換算して走行速度と旋回速度について考える．

　　　                                                (2-1-1)

　　　                                                (2-1-2)

・誤差とその積分要素を旋回速度にフィードバックする．

　　　             (2-1-3)

　とする．

・走行速度は一定とする．

・誤差に関する運動方程式は

　　　                                     (2-1-4)

　　　，　　    (2-1-5)

・誤差が小さいとして線形化する．

　　　                                         　　　 (2-1-6)

　　　     　　(2-1-7)

・Δθについてまとめると

　　　                        (2-1-8)

・前記のG(s)は

　　　                              (2-1-9)

　（この形はサンプル値制御に利用する）

・系の特性方程式は

　　　　　　　　　　 　　　 (2-1-10)

・系の特性を

　　　　→　       (2-1-11)

　となるようにゲインを決める．

　　　，　，　         (2-1-12)

　　　，　　 →　        (2-1-13)

　∴　                                                               (2-1-14)

・上式が根を持つためには根号内が正であることが必要である．

　　　

　　　　                                              (2-1-15)

　　∴　                                                           (2-1-16)

　ωnとαは独立には設定できない．

・根は２つあるが大きい方を採用する．すなわちゲインは

　　　　，　，　       (2-1-17)

 

（２）　1FDW1FS機構のPI制御のゲイン

 

・目標経路は分かっているとする．駆動輪速度vdは一定とし，誤差フィードバック制御は行わない．

・誤差は経路ずれとステアリング(ST)角誤差であり，ST速度にフィードバックする．

　ST角誤差は，経路が既知であるからどの地点で指令のST角φcが分かっており，である．

・誤差とその積分要素をステアリング(ST)速度にフィードバックする．

　　　    (2-2-1)

・誤差に関する運動方程式は

　　　                                      (2-2-2)

　　　，　，　        (2-2-3)

・誤差が小さいとして系を線形化する(Lはトレッド)．また指令の走行速度は

　　　                                                 (2-2-4)

　である．Laplace変換して

　　　                                        (2-2-5)

　　　                         (2-2-6)

　　　  (2-2-7)

・特性方程式は

　　　

　　　   (2-2-8)

・系の特性を

　　　　→　   (2-2-9)

　となるようにゲインを決める．

　　　                                    (2-2-10)

　                (2-2-11)

　                  (2-2-12)

　                              (2-2-13)

これらからKIだけの式に変形する．第４式，第３式より

　                                    (2-2-14)

　                 (2-2-15)

　第２式に代入

　　　    (2-2-16)

　∴　　→　   (2-2-17)

　　　            (2-2-18)

　すなわち各ゲインは

　　　，　　後者は通常ζ≒1程度なので採用しない． (2-2-19)

　　　                           (2-2-20)

　　　                                (2-2-21)

　である．

・であるから，ST角φcによって（ωn,ζ）が異なり，φc≠0のときはφc=0のときより小さい．仮にφc=0としてゲインを決め一定に保つとすると，φc≠0のときは（ωn,ζ）を小さめに設定したことになり，これは応答性は悪くなるが安全側である．

 

（３）1RDW1FS機構のPI制御のゲイン

 

・1FDW1FS機構と同様に，誤差は経路ずれとステアリング(ST)角誤差であり，それらの誤差とその積分要素をステアリング(ST)速度にフィードバックする．

　　　，　    (2-3-1)

・駆動輪速度vdは一定とする．

　　　                                                    (2-3-2)

・誤差に関する運動方程式は

　　　　　　　　　　　　　　　　              (2-3-3)

　　　，　　，　      (2-3-4)

・誤差が小さいとして系を線形化し，Laplace変換すると(Lはトレッド)．

　　　                                              (2-3-5)

                                   (2-3-6)

　　　     (2-3-7)

・この式はL→と置くと1FDW1FS機構と同じであり，特性方程式とゲインも同様に決まる．

　　　                                             (2-3-8)

・特性方程式は

　　　          (2-3-9)

・1FDW1FS機構と同様に系の特性を

　　　　→　    (2-3-10)

　となるようにゲインを決める．

・前項を参照して

　　　，　　後者は通常ζ≒1程度なので採用しない．        (2-3-11)

　　　                             (2-3-12)

　　　                                   (2-3-13)

・であるからゲインはφcによって（ωn,ζ）が異なり，φc≠0のときはφc=0のときより大きい．仮にφc=0としてゲインを決め一定に保つとすると，φc≠0のときは（ωn,ζ）を大きめに設定したことになり，線形化理論では安定であるが，AGV運動の非線形性によって不安定となる可能性がある．

 

３．経路追従制御のソフトウエアサーボ

 

・AGVの経路追従制御にコンピュータによるソフトウエアサーボが許されるとすれば，より安定性・収束性の良い制御法を考えることができる．

（１）ST角によってゲインを変更する．ゲインは本来指定ST角φcに依存しているが，線形化系ではφc=0として一定値とした．

（２）誤差大きいときはP制御，小さくなったらPI制御と切り替える．

（３）遠いときは経路最近点へ円弧―直線（クロソイド−直線）による経路生成，次にP制御，最後にPI制御とする．

　などが改善策の例である．

 

［シミュレーションの使い方］

 

（１）使用フォルダー名：3-12-3AGVFBC0 ( プログラム名AGVFBC0.c, graph2d.h )

（２）文字画面でのキー操作

　(1)スタート → (2)経路(0,1)の選択 → (3)FB系の固有振動数・減衰比設定 →  (4)AGVの初期状態設定

 （(5)３種走行制御の運動計算）→ 任意キーによって描画画面へ

　　　　　　 → 描画画面からの変更があるとき(2), or (3) or (4)へ

  [註] 描画画面で初めに2DW1C機構のアニメーションを描画するように設定している．

（３）描画画面での表示

　(1) 中央面にAGVの走行経路と運動アニメーション図

　(2) 右上に経路誤差(Δd，Δθ)の位相平面トラジェクトリのグラフ

（４）描画画面でのキー操作

　以下はそのまま描画画面に留まる．

　‘s’：上記運動の時間経過（sを押し続けると時間的に変化する）

　‘0’：運動を始点に戻す

　‘x’ , ‘X’, ‘y’, ‘Y’：アニメーション画面を左右上下に移動

　‘w’, ‘W’：アニメーション画面を縮小拡大

　‘z’, ‘Z’ ：位相平面図を左右に移動

　‘1’, ‘2, ‘3’ ：アニメーション描画のAGV選択

　‘P’,’I’：P＝Ｐ制御（青），I=PI制御(緑)の描画選択

　以下は文字画面に戻る．

　‘c’　 ：経路変更のために文字画面(2)へ

　‘f’　 ：FB系のゲイン（固有振動数・減衰比）変更のために文字画面(3)へ

　‘h’ 　：AGVの初期状態変更のために文字画面(4)へ

　‘ESC’：終了

［註］FB系の設定値で２つ目の減衰係数はα=ωnまたは安定範囲内のできだけ大きな値とする．

計算を済ませてから画面表示する．

計算には数秒かかることがある．

 

・シミュレーションの固定した条件は，AGVのホイールベースとトレッドL=B=1[m]，駆動輪速度vd=1[m/s]，ST限界速度ωmax=3 [rad/s]，ST最大角度φmax=3[rad]である．ωmaxとφmaxが運動の安定性に影響する．

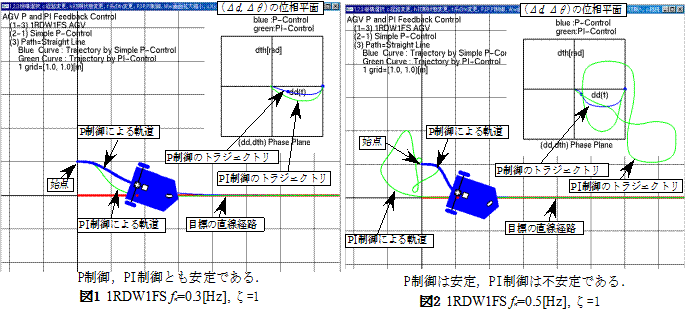
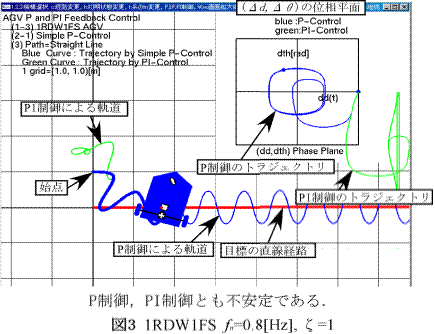
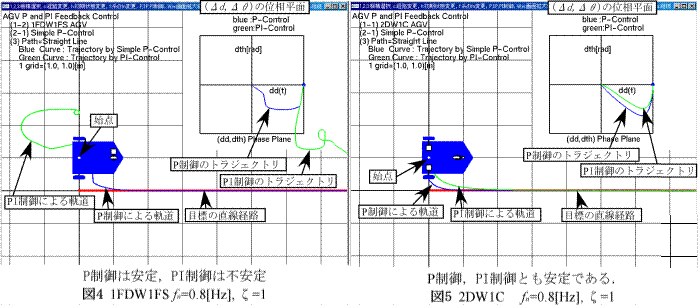
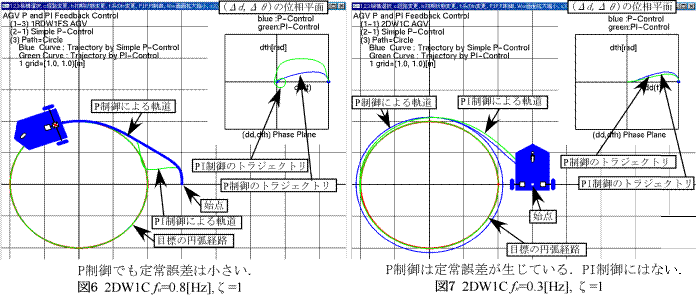
・以下の図は1RDW1FS機構の経路追従安定性と，2DW1C機構の定常経路誤差の例を示している．

・図１〜３は1RDW1FS機構が直線経路追従する制御で，FB系の固有振動数fnが大きくなる（ゲインが大きい）と運動が不安定になっていく様子を示している．

・不安定とは，指定経路に収束しない場合と，途中で１回転したり，大幅に反対方向に走るなどの場合を言う．

・線形化したFB系は安定であるが，誤差が大きい（初期状態が経路から離れている）と，非線形性が強くなり指定経路に収束しない．

・不安定の要因は，第１に運動の非線形性にある．すなわち誤差が大きいと線形化系の安定性が損なわれる．

・第２にステアリング速度の頭打ちがある（この例ではωmax=3[rad/s]，駆動輪速度vd=1[m/s]）．ゲインが高いと少しの誤差でST速度ωがωmaxに達し，系はON-OFF制御のようになってチャタリング現象が生じ，安定しない．

・不安定要因の第３は1RDW1FS固有の特性による．すなわちST角φが90°近いと駆動速度を一定に保っているので旋回速度が異常に大きくなり（），急激に向きθが変わる．この異常な変化が不安定性を増す．

・1FDW1FS機構では旋回速度は大きくはないので（）1RDW1FS機構よりFB系の固有振動数を高くすることができる．

・ST付きAGVの積分要素は系の不安定性を増す．

・図４，５は1RDW1FS機構が不安定であるfn=0.8[Hz]の場合でもP制御は安定であることを示している．安定性から見れば，2DW1Cが最もよく，1FDW1FSがそれに次ぎ，1RDW1FSは最も悪い．

・図６，７は2DW1C機構の円弧経路への追従性を示している．P制御では系の固有振動数が低いと定常誤差が生じているが，積分要素を加えたPI制御では定常誤差がない．

・2DW1Cは積分要素がないと定常誤差が無くならない（図では指定経路より大き目の円を描く）．すなわち積分要素は不可欠である．

・固有振動数を高くすれば（ゲインを高くすれば）定常誤差を差し支えない程度に小さくすることができる．

・一方ST付きAGVは積分要素がなくても最終的に誤差０で円弧に追従する．

・これはST角に旋回の積分性があるからであり，一定曲率に対して定常誤差が生じない．

・ST付きAGVには積分要素は不要である．

・ただしST付きAGVでは曲率の急激な変化に追従するには積分要素が有効である．しかしこの元々AGVの運動が非線形であり，系が複雑になれば不安定になり易く，積分要素は勧められない，

 [註１]

・誤差が０以外の値に収束する可能性がある（位相平面解析では原点以外に特異点があると言う）．

・例えば2DW1C機構の誤差に関する制御方程式は

　　　，　

　であり，もし

　　　±(2n-1)π or ±2nπ,　

　ならば，となり，上記の値が定常誤差として残る．±(2n-1)πの系列は不安定特異点であるが，±2nπの系列は安定特異点である．初期位置姿勢が目標と大きく異なる場合この特異点に収束する可能性がある．同じ状況が他の場合にも存在する．

・Δθが±2πになったら０に戻すという操作をすれば上記特異点に収束することはなくなる．ただしPI制御の場合，誤差の積分の取り方に不連続性が生じ，正しいPI制御はできない．

[註２]

・このシミュレーションでは「安定領域」を示していないが，その結果は「詳説ロボットの運動学」10.6.2節の結果（図10.31）とやや異なる．これはここではST速度に制限を設けているからである．

 

 

［AGV経路誤差フィードバック制御の特徴］

 

・FBゲインが大きければ経路追従性が良くなるが，大き過ぎると不安定になる．

・それはAGV運動の非線形性，ST速度の頭打ちのためである．

・2DW1Cでは，誤差を旋回速度Ωにフィードバックするが，定常誤差をなくすために積分要素が必要である．

　（積分要素がないと常に経路目標に遅れて追従する）

・ステアリング付きAGVでは積分要素は必要ない．

・制御の安定性・即応性から見て，2DW1C，1FDW1FS，1RDW1FSの順に優れている．