１２．３１ 移動ロボットのフィードバック制御シミュレーション１ ２００８−７−１０
実行ファイル AGVFBC1exe
目次
１．AGV機構
２．経路
３．経路制御のいくつかのパターン
３．１ 経路既知（AGVが知っている場合）の経路誤差フィードバック制御
３．２ 経路未知（AGVが知らない場合）の経路誤差フィードバック制御
３．３ 経路未知で経路曲線を推定しながらの経路誤差フィードバック制御
４．制御系の解析
４．１ 2DW1C機構の制御方程式
４．２ 1FDW1FS機構の制御方程式
４．２．１ 経路既知，または経路曲率を推定する場合
４．２．２ 経路未知の場合
４．３ 1RDW1FS機構の制御方程式
４．３．１ 経路既知，または経路曲率を推定する場合
４．３．２ 経路未知の場合
５．経路制御シミュレーション
［シミュレーションの使い方］
［AGV経路制御の特徴］
・指定した経路があり，時間に関係なく経路R(s)を辿る制御を「経路制御(path control)」と呼ぶことにする．
・時間も指定した経路（軌道）R(t)を辿る制御を「軌道制御(trajectory control)」と呼ぶ．
・AGVが経路を知っている場合，機構誤差などがないとここでは仮定しているので，R(t)を指令値として与えれば正しい軌道を辿り，フィードバック制御の必要がない．
・機構誤差・滑りなどがあり，R(t)を指令値として与え誤差をフィードバックする制御は12.32AGV機構誤差のフィードバック制御（ファイル名 3-12-32AGVerrFBC，フォルダ名 3-12-32AGVerrFBC ）で論じる．
・ここでは（１）経路が分かっているときは指令駆動輪速度を与え経路誤差フィードバックする経路制御，未知のときは（２）一定駆動輪速度で経路誤差をフィードバックする経路制御、（３）過去のデータから経路曲率を推定し、その変化率から駆動輪速度を変え，経路誤差をフィードバックする経路制御の3種の制御法について、経路追従性をシミュレーションする．
１．AGV機構
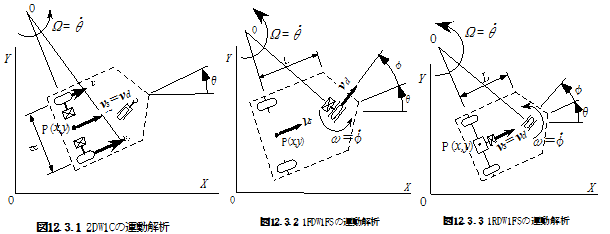
・移動ロボット(AGV)の機構は
（１）2DW1C（２駆動輪とキャスタ）
（２）1FDW1FS（前輪駆動と前輪ステアリング）
（３）1RDW1FS（差動歯車付き後輪駆動と前輪ステアリング）
の３種とする（いずれも大きさ約1m）．
・駆動輪速度とステアリング角速度には限界がある（Vmax=2[m/s]，ωmax=3[rad/s]）．
・駆動・旋回速度は不連続に変化させることができる（急速変化が可能である）．
・原則的に駆動輪速度vdはVw=1[m/s]とする．
但し，急旋回の局部ではステアリングが間に合うように速度を落とす．
・経路のずれは，AGV代表点とその前方D離れた点の２ヶ所に経路センサがあり，経路ずれΔdと角度ずれΔθがセンシングできるとする．（図12.3.2）
［註］２つのセンサの間隔Dが大き過ぎると，経路が曲がっているときには角度の誤差が生じる．急なカーブを正しく計測したければ，センサを３つ以上付ける方がよい．
２．経路
・経路を辿るだけでよい走行制御を「経路制御」と呼び，時間関数として走行距離も正確である走行制御を「軌道制御」と呼ぶ．
・経路は
，
，総称して
と，経路長sの関数として表現する．
・指令軌道の走行速度は，急カーブで旋回可能なように曲率κによって変えるとする．
・指定された経路をAGVが予め知っている場合と，分かっていない場合についてシミュレーションを行う．
・以下で経路ずれをΔd，角度誤差をΔθ，ステアリング角度誤差をΔφとし，３誤差を合わせて
と表す．この誤差をフィードバックして経路追従させる．
３．経路制御のいくつかのパターン
・経路に沿う走行距離は正確でなくてもよいので，ΔRのみを旋回（またはステアリング）にフィードバックする．
・走行速度は定速か，旋回曲率に応じた可変速とする．
・経路既知（AGVが予め知っている）ときは，経路曲線の曲率κ，その変化率
が分かっているのでそれらに応じて走行速度を変えることにする．
・経路を辿る理論的な時間変化
を生成し，
に対応するAGVの制御変数
を生成することができる．（の生成は12.1CP曲線の具体例（ファイル名 3-12-03CP ）を参照のこと．
・AGV機構に誤差がなければ理論のを与えれば理論通りの経路を辿り，誤差フィードバックの必要がない．
（誤差があれば理論のに誤差フィードバックの
を加えるＦＦ制御とすることができるが，ここではを生成せず，誤差フィードバックのみによって経路追従する制御法を考える．
・κ’が既知または推定できるときは駆動輪速度を可変とし，未知のときは駆動輪速度＝一定とする．
３．１ 経路既知（AGVが知っている場合）の経路誤差フィードバック制御
・経路曲線の曲率とその変化率が分かっているので，それに応じて走行速度を変える．（2DW1C機構では如何なる急旋回も可能で，一定走行速度としてよい）
・ステアリング(ST)付きAGV機構では，駆動輪速度
とST速度ωとは
(3-1)
（1FDW1FS）， 
（1RDW1FS）
(3-2)
（LはAGVのトレッド，φはST角）
の関係にある．
・ωはωmaxを超えられないので，Aが大きいときは正しく旋回できるようにvdを小さくしなければならない．
・経路既知のときは，経路に沿うAが分かっているのでωがωmaxを超えないときは
，超えるときは
の走行速度とする．
・理論的なST角φも分かっているので，フィードバックする誤差はである．
３．２ 経路未知（AGVが知らない場合）の経路誤差フィードバック制御
・経路が未知のときはκ’が不明なので駆動輪速度を一定とする．
・理論的なST角は未知なので，フィードバックする誤差は
である．
・急旋回のときに経路から大きくはずれる可能性があり，危険な制御であるが，フィードバックゲイン，経路によってどれだけついていけるか見るために試みる．
３．３ 経路未知で経路曲線を推定しながらの経路誤差フィードバック制御
・過去の情報からκ’を推定し，その結果を以て駆動輪速度を可変とする．
・厳密に言うと，Dead ReckoningによってAGV自身の角度θを得，センシングしたΔθを引き算して理論経路のθcを求める．そのθcのサンプル時間Δt間の変化からκを求める．そのまた時間変化からκ’を推定する．
， 
， 
(3-3)
・AGVの誤差がなければ，この計算で正しいκ’が得られ，制御性も3.1節と同じであるが，実際には２次の差分をとる計算は誤差の影響を受け易い．
・誤差があるときのこの方法の妥当性は別の節で論じる．
・理論的なST角φも推定できるので，フィードバックする誤差はである．
４． 制御系の解析
・制御系の解析は既に12.30経路追従のフィードバック制御の基本（ファイル名 3-12-30AGVFBC0 ）で述べた．ここでは結果のみを示す．
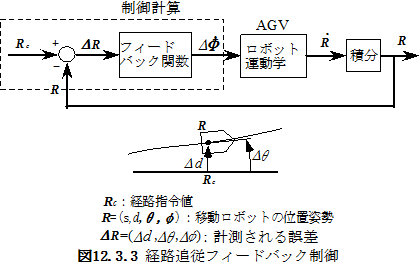
・経路曲線を経路長sの関数として
と表す．
・制御変数は２つの駆動輪速度，または駆動輪速度とST速度である．
４．１ 2DW1C機構の制御方程式
・このAGV機構はどんな急旋回も可能なので，走行速度vsは一定でよい．
・経路が未知でも既知でも，制御方程式は同じである．
・（走行速度vs，旋回速度Ω）と２つの駆動輪速度
の換算は容易である．
， 
(4-1)
・ここでは走行速度＝一定とし，経路誤差
は旋回速度Ωにフィードバックする．
・定常誤差をなくすために積分要素を加える（これがないと定常速度誤差が生じる）．
(4-2)
・線形化式の特性方程式は３次遅れ系であり，
(4-3)
と表すことができる．
・系の固有振動数・減衰比・２つ目の減衰係数を
とするには
， 
， 
(4-4)
(4-5)
， 
， 
(4-6)
となる
とすればよい．
φはキャスタ角を表すが，制御には関係ない．
４．２ 1FDW1FS機構の制御方程式
４．２．１ 経路既知，または経路曲率を推定する場合
・経路の曲率とその変化率が分かる（推定できる）ので，ST速度の限界を考慮して駆動輪速度を変更し，追従性を良くする．
・駆動輪（前輪）速度をvdとすると，走行速度と旋回速度は
， 
(4-11)
・経路誤差
，
をST速度にフィードバックする．
(4-12)
・ST角制御に積分性があるのでここでは比例制御(P制御)のみとする．
・線形化した系の特性方程式は３次遅れ系であり，
(4-13)
と表すことができる．
・系の固有振動数・減衰比・２つ目の減衰係数をとするには
， 
， 
(4-14)
すなわち
， 
， 
(4-15)
とすればよい．
４．２．２ 経路未知の場合
・走行速度（駆動輪速度）を一定とする．
・ST速度が間に合わないと分かったとき速度を下げる方法もあるが，ここでは簡単のためにvd=一定とする．
・経路未知であるから，目標とすべきST角φc（曲率κに依存）が未知であり，ST角の誤差FBができない．
・上式でST角誤差FBをなくす（
とする）と，系は不安定となるので，別のFB方式を考えなければならない．
・その方式は以下の通りである．
（１）誤差を旋回速度ΩにFB（Ωfとする）
（２）ΩfをST角φfに換算（(4-18)式）
（３）ST角をφfとするために，前のφデータと比較してST速度ωを算出
（４）そのωを指令値とする．ただし
・式で表すと
(4-21)
(4-22)
前回（サンプル時間dt前）のST角をφbとすると
， ただし
(4-23)
・ならば，この系は2DW1Cと同じであり，系の固有振動数・減衰比・２つめの減衰係数をとするには
， ， (4-24)
(4-25)
， ，
(4-26)
となるとする．
・走行速度vsは
であり，φによって変わるが，ここではφ=0，すなわちvs=vdとしてゲインを決める．
・
ならば
で頭打ちとなり，旋回速度はΩfを出せない．
・FBゲインが大きいと頭打ちの頻度が高くなり，ほとんどBang-Bang制御となる．これは不安定になり易い．
・この未知経路の制御では安定性のために，駆動輪速度を通常より下げること，及びFBゲインを下げることが望ましい．
４．３ 1RDW1FS機構の制御方程式
４．３．１ 経路既知，または経路曲率を推定する場合
・駆動輪速度（後輪車軸中点）をvdとすると，走行速度，旋回速度は
， 
(4-31)
・経路誤差をST速度にフィードバックする．
(4-32)
・ST角制御に積分性があるのでここでは比例制御(P制御)のみとする．
・線形化した系の特性方程式は
(4-33)
と表すことができる．
・系の固有振動数・減衰比・２つ目の減衰係数をとするには
，
， (4-34)
すなわち
， 
，
(4-35)
とすればよい．
４．３．２ 経路未知の場合
・走行速度（駆動輪速度）を一定とする．
・制御方式は1FDW1FS機構と同じである．
(4-36)
(4-37)
前回（サンプル時間dt前）のST角をφbとすると
， ただし
(4-38)
・ならば，この系は2DW1Cと同じであり，系の固有振動数・減衰比・２つ目の減衰係数をとするには
， ， (4-39)
(4-40)
， ，
(4-41)
となるとする．
・走行速度vs=vdである．
・ならばで頭打ちとなり，旋回速度はΩfを出せない．
・FBゲインが大きいと頭打ちの頻度が高くなり，ほとんどBang-Bang制御となる．これは不安定になり易い．
・この未知経路の制御では安定性のために，駆動輪速度を通常より下げること，及びFBゲインを下げることが望ましい．
５．経路制御シミュレーション
移動ロボット(AGV)の指定した経路を追従する経路制御のシミュレーションを行う．
● シミュレーションには以下の仮定を置く．
・移動ロボット(AGV)の機構は
（１）2DW1C（２駆動輪とキャスタ）
（２）1FDW1FS（前輪駆動と前輪ステアリング）
（３）1RDW1FS（差動歯車付き後輪駆動と前輪ステアリング）
の３種とする（いずれも大きさ約1m）．
・駆動輪速度とステアリング角速度には限界がある（Vmax=2[m/s]，ωmax=3[rad/s]）．
・急カーブでない通常の駆動輪速度をVwとする（Vw=1[m/s]）．
・経路未知で曲率推定しない場合の駆動輪速度は，更に速度を下げる（Vw=0.5[m/s]）．
・旋回速度は不連続に変化させることができる（急速速度変化が可能である）．
・空間には障害物がない．
・AGVは経路からのずれ
・方向角誤差
のセンシングができるとする．（GSP・灯台方式による絶対位置姿勢，誘導線センシングによる相対位置姿勢等の計測法が考えられる）
● 指定経路
・経路は直角座標表現
，極座標表現
の曲線10数種が用意されており，この中から選ぶ．（新しい曲線指定はできない）
・曲線を選び，大きさなどの諸元を指定する．
・経路長の限界は約15[m]である．
●制御法
・経路制御は経路からのずれと方向角誤差を2DW1Cでは旋回速度Ωに，ST付きAGVではST速度ωにフィードバックする（経路未知では間接的なFB．4.2.2，4.3.2節参照）．
・ST速度には限界があることを考慮する．
（FBゲインを大きくしても飽和値に達すると例えば急カーブを回り切れないことがあり，これが制御性を大きく損ねることがシミュレーションによって分かるであろう）．
● 走行速度の時間的変化
・このことを考慮して，走行速度（駆動輪速度）一定・可変の制御性の比較を行う．
（１）指定経路をAGVが知っており，その経路の曲率によって走行速度を可変とする制御
通常は一定速度で走行し，ST速度が間に合わないときに走行速度を下げる(4.1，4.2.1．4.3.1節参照)
（２）指定経路をAGVは知らず，走行速度＝一定とする制御（4.2.2，4.3.2節参照）
（３）指定経路をAGVは知らないが，過去のデータから曲線の曲率を推定し，それによって走行速度を加減する制御（4.2.1．4.3.1節参照）
・走行速度可変はST付きAGVに適用され，2DW1Cには必要がない（急旋回が可能である）．
・（１）はST速度ωmaxが間に合うように速度を落とすので正しい経路追従できるように思えるが，FBゲインが低いと追従できないこともある．
・（２）は好ましくない制御法であるが，比較のためにシミュレーションする．緩やかな曲線ならばこれでも十分追従精度が良いことが分かる．
・（３）は曲率推定の精度がどれだけ制御性に影響するかを，（１）との比較で調べる．
［シミュレーションの使い方］
（１）使用フォルダ名：AGVFBC1 ( プログラム名AGVFBC1.c, graph2d.h )
（２）文字画面でのキー操作
(1)スタート → (2-1)経路の選択 → (2-2)経路諸元設定 → (3)FB系の固有振動数設定
（(4)３種走行制御の運動計算）→ 任意キーによって描画画面へ
→ (4)描画画面からの変更があるとき(2)へ
（３）描画画面での表示
(1) 左半面にAGVの走行経路と運動アニメーション図
(2) 右上・中にAGVの位置
の変化とx,y各方向のずれのグラフ
(3) 右下に経路からのずれのグラフ
（４）描画画面でのキー操作
以下はそのまま描画画面に留まる．
‘s’：上記運動の時間経過（sを押し続けると時間的に変化する）
‘0’：運動を始点に戻す
‘x’ , ‘X’, ‘y’, ‘Y’：アニメーション画面を左右上下に移動
‘w’, ‘W’：アニメーション画面を縮小拡大
‘1’, ‘2, ‘3’ ：アニメーション描画のAGV選択
‘P’,’d’,’D’：P=経路既知・可変走行速度，d=経路未知一定走行速度，D=経路未知曲率推定 の描画選択
以下は文字画面に戻る．
‘c’ ：経路変更のために文字画面へ
‘f’ ：FB系のゲイン変更のために文字画面へ
‘ESC’：終了
［註］どのAGVもホイールベース・トレッドは約1mであり，変更しない．
系の減衰比はζ=1，２つ目の減衰係数α=ωnまたは安定範囲内のできだけ大きな値とする．
計算を済ませてから画面表示する．
計算には数秒かかることがある．
経路長長過ぎるときは中途で「計算を中止」のメッセージを表示し，経路選択に戻る．
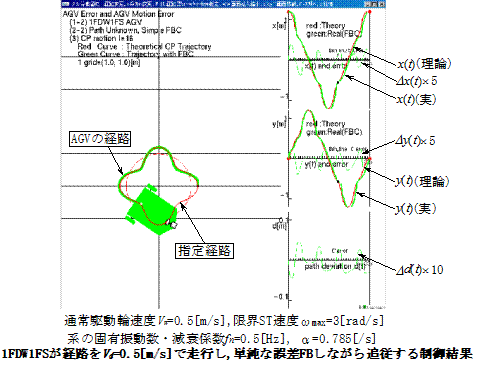
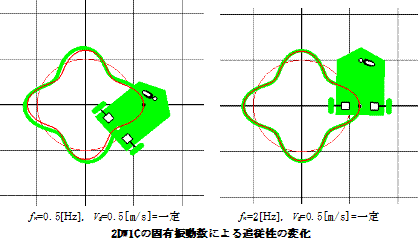
・以下の図は経路を1FDW1FS機構と2DW1C機構のAGVが経路追従する例を示している．
・図の
のグラフは，実軌道とそれが参照する経路上の最近点との差であり，理論値（赤線表示）との差ではない．
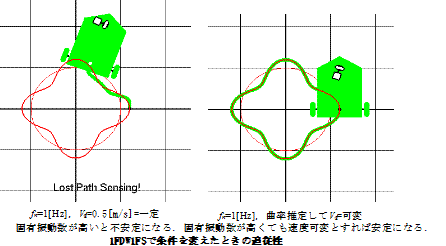
・1FDW1FSが経路推定せずに一定速度で走行する場合，FBゲインが小さいとST速度の飽和が生じ難く，良好に追従する（上図）．
・ゲインを上げると，急旋回のときにST速度が飽和してついていけず，不安定となる（中左図）．
・経路曲率推定変速走行の場合は，ST速度が間に合わないときに速度を下げることをしているので，経路追従性は良好であり，ゲインが高い程よくなる（中右図）．
・この結果は曲率推定がほぼ正しいことも示しているが，これはAGV機構に誤差がなく，滑りもない理想状態で推定しているからで，実際のこれらの誤差を含む走行制御にも有効かどうか，この段階では分からない．
・2DW1Cでは一定駆動輪速度でも大抵の場合は経路追従する．またゲインが高いほど良好である（下図）．
［AGV経路制御の特徴］
・当然のことながら，FBゲインが大きければ追従性が良くなる．
・ただし，ST速度の限界のために大き過ぎても，効果がないだけでなく，却って不安定の原因ともなる．
（これは制御一般に言える現象である）
・2DW1Cでは，誤差を旋回速度Ωにフィードバックするが，定常誤差をなくすために積分要素が必要である．
（積分要素がないと常に経路目標に遅れて追従する）
・曲率変化が大きい経路では，定速走行は誤差が大きく，または経路を見失うこともある．
・経路の曲率変化の推定は，変化が大きいときにやや真値と異なるが，その推定誤差は制御性を損なうことはない．
・ただし，これは理想状態の推定であり，実際のAGV機構誤差や車輪の滑りなどがあるときも大丈夫かどうか分からない．
・1FDW1FSでは，
であり，
以上の旋回速度を出せない（他のAGV機構ではΩに限界がない）．経路未知で，4.2.2，4.2.3節のようにΩからωを決める方法では，Ωの限界とωの限界の両方を考慮しなければならず，そのため制御性が他の機構より悪い．
・AGVの機構は，制御性から見ても2DW1Cが優れていることが分かる．