３　　線形ｎ自由度振動系の自由振動(03freevibrationn)

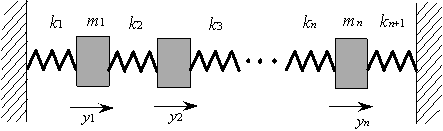・　n自由度の自由振動は，n個の固有振動数があり，それぞれに対応する固有モードがあること，および任意の初期条件から始まる振動はn個のモードの適当な比率を掛けた和であることが見られる．

・　運動方程式は

　　

　　

　　・・・・・・・・・・・・・・・

　　

　　・・・・・・・・・・・・・・・

　　

・ 自由振動を

と置くと，上式は

，すなわち

ただし　，　

の全てが０でない解を持つためには

　　

この式はに関するn次式であり,

と表せる．この式を振動数方程式という．この式の根が固有振動数であり，一般にn個存在する．

・ i次の固有振動数に対応する振動振幅は，各マスの振幅比として得られる．例えばとしてはに対する比として

　　，　

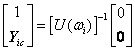により与えられる．この振幅比をi次の振動モードと言う．

・ 各モードには

　　　　，　　

　　の性質がある．これを各モードは直交すると言う．この性質を利用して任意の初期条件から始まる自由振動は

　　　　

　　のようにモードの線形和で表すことができる．

● シミュレーションにおける描画画面

・ 画面左側　：　振動の時間経過（描画画面上でキーsを押し続けると時間的変化が表示される）

右側　：　弦でつながったマスの振動モード

● シミュレータの使い方

・ スタート → (1)自由度入力 → (2)系の定数入力 → (3)描画する振動波形の数入力

→　(4)初期条件設定 →　描画

・ キー操作（描画画面上でキーを押し，変更は文字画面上で）

s    ：振動継続（sを押し続けないと何も変化しない）

n    ：自由度変更

m   ：自由度変えず，系の定数変更

j    ：上記系を変えず，初期条件変更

c    ：描画する振動曲線の数変更

Y, y  ：振動振幅の拡大縮小

T, t  ：時間軸の拡大縮小

●　特徴

(1) 振動モードは最小の固有振動数ではマス全体が１つの半波長のようになる．と次数が高くなるにつれて２つ，３つ，･･･の半波長の波が見られ，第n次モードはマスが順にプラス・マイナスに位置するn個の半波長が見られる．