４　　線形１自由度振動系の強制振動（１）−外力作用の場合−( 04forcedvibration11 ）

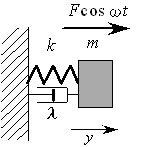
・　強制外力に対するマスの応答が振動数によって如何に変わるかを見る．

・ 運動方程式は

　　

・ マスの定常振動は

　　 ，　

　　　（固有振動数）, （減衰比） （振動数比）

　　と置くと

・　が周波数特性を表す．

● シミュレーションにおける描画画面

・ 画面左側　：　振動の時間経過（描画画面上でキーsを押し続けると時間的変化が表示される）

右側　：　マスの振動と系の周波数特性（キーfを押した場合）

● シミュレータの使い方

・ スタート → (1)系の定数入力 → (2)外力条件入力 → (3)初期条件設定 → 描画

・ キー操作（描画画面上でキーを押し，変更は文字画面上で）

s    ：振動継続（sを押し続けないと何も変化しない）

m   ：系の定数変更

g    ：系の定数変えず，外力条件変更

j    ：上記系を変えず，初期条件変更

f    ：周波数特性描画

X, x ：スペクトルの横軸拡大縮小

T, t  ：振動曲線時間軸拡大縮小

Y, y ：振動・周波数特性の縦軸拡大縮小

●　特徴

(1) のとき共振振幅のピークが見られるが，ではピークがない．

(2) が共振点であるが，ではピークはのときに生じ，その振幅は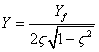である．

(3) ，のとき，共振振幅は無限大であるが，有限の初期条件から始まる振動は振幅が（振動の包絡線が）直線的に増加する．

(4) ，のとき，振動は唸りを生じながら徐々に定常振動に近づく．