７　　線形２自由度振動系の強制振動（２）−動吸振器問題−（Forcedvib22）

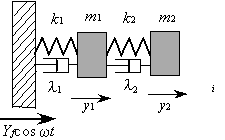
・ ベースの振動をマスの先に付加した第２のばねマス系によって第１マスの振動を減らす動吸振器の問題である．

・ 運動方程式は

　　

　　

・ ２つのマスの定常振動は

　　，　，　

　　，　　，　　

　　，　　，　　

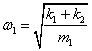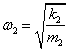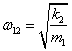
　　と置くと

　　

　　　

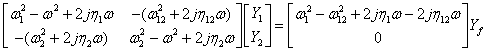
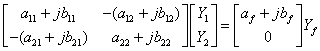
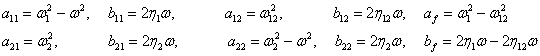
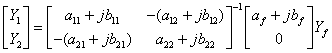
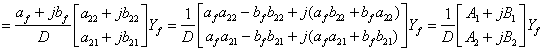
　　となる．

　　　

　　　

　　　

　　　，　

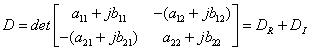
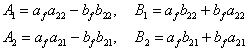
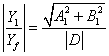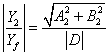
・　付加した第２のばねマス系の固有振動数を外力振動数と等しくし（），その系の減衰を小さく（すなわち，）すれば，第１マスの振動は小さくなる．これが動吸振器の原理である．

● シミュレーションにおける描画画面

・ 画面左側　：　振動の時間経過（描画画面上でキーsを押し続けると時間的変化が表示される）

右側　：　弦でつながったマスの振動モードと系の周波数特性（キーfを押した場合）

● シミュレータの使い方

・ スタート → (1)系の定数入力 → (2)外力条件入力 → (3)初期条件設定 → 描画

・ キー操作（描画画面上でキーを押し，変更は文字画面上で）

s     ：振動継続（sを押し続けないと何も変化しない）

m    ：系の定数変更

g    ：系の定数変えず，外力条件変更

j    ：上記系を変えず，初期条件変更

f    ：周波数特性描画

X, x ：スペクトルの横軸拡大縮小

T, t  ：スペクトルの横軸拡大縮小

Y, y ：振動・周波数特性の縦軸拡大縮小

● 特徴

(1) 付加する第２ばねマス系のダンパーを０とすると（固有振動数，），第１ばねマス系の定数が何であってものベース振動に対して振動振幅は０となることが分かる．

(2) この場合，が小さければ第１マスの振動は小さい．

(3) が小さければ上記の場合，第２マスの振動振幅は大きくなる．これは例えば建物の地震に対する振動を動吸振器によって防振するとき，小さな第２ばねマス系では防振できないことを意味する．

(4) 動吸振器は「地震による建物の揺れのエネルギーを第２マスの振動で吸収する」と解釈され，第２マスが小さいと吸収し切れないからである．

・ 上記の場合，シミュレーションで第２マスの振動はベースの振動と逆位相であり，ベースの揺れからの力を第２マスの揺れが相殺していることがわかる．