９　　スペクトル解析（１）−周期波形のスペクトル−（09spectrum1）

・ 周期関数は基本振動数の倍数の振動数の重ね合わせからなる．

・ それぞれの振動数の振幅はいくらであるかを知るのがFourier解析（スペクトル解析）であり，それらの振動を合成して（重ね合わせて）元の波形を再現するのがFourier逆変換である．

・ このシミュレーションンでは，

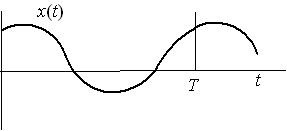
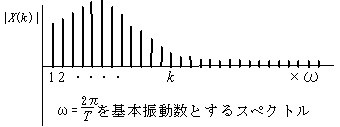
（１）周期波形をFourier解析して，スペクトル

　を求める．

（２）有限のスペクトル成分の振動を合成して

元の波形を再現する．

・ スペクトルの全ての正弦波を合成すれば元の波形が再現できる．もし有限のスペクトル正弦波を合成すれば波形がどのように歪むかを調べる．

・ 周期波形のFourier展開（スペクトル解析）

周期波形をとするとスペクトルは

　（単位は波形と同じm）

　，　　

・ 有限スペクトルの合成（Fourier逆変換）

　　

である．

［補］Fourier展開計算の数値積分に関する注意

　一般的に数値積分には台形則，Simpson則（２次関数近似），３次関数近似等々があり，高次ほど誤差が小さくなる．しかしFourier積分には台形則以外は使えない．Simpson則以上の高次近似ではスペクトルのfoldingが生じる．例えばωの振幅１の単一正弦振動をSimpson則によってFourier積分すると，ωm−ωの振動数に1/3の振幅があるかの如き結果が得られる（ωm=π/Δt）．３次以上でも別の振動数に０でない振幅が生じる．Foldingが生じないのは台形則だけであり，精度が悪いがやむを得ない．

● シミュレーションにおける描画画面

・ 画面左側　：　原周期波形と有限数スペクトルを合成した再現波形

右側　：　スペクトル（線スペクトル）

● シミュレータの使い方

・ スタート → (1)周期波形の選択 → (2)波形合成するスペクトル数設定 → 描画

・ キー操作（描画画面上でキーを押し，変更は文字画面上で）

m    ：別の波形選択（自作の周期データを使うこともできる）

n    ：合成スペクトル数変更

t, T  ：波形の時間軸拡大縮小

y, Y  ：スペクトルの縦軸拡大縮小

x, X  ：スペクトルの横軸拡大縮小

●　特徴

(1) 滑らかな波形は少ないスペクトル数で元の波形を再現できる．

(2) 不連続性がある波形では，スペクトル数をかなり多くしても不連続部分で元の波形との違いが目立つ．

(描画の時間軸を拡大するとよくわかる)

(3)  AM変調波形は，（変調振動数）＋（非変調・信号振動数）以上のスペクトルで元波形を再現できる．すなわちAM変調ではの狭い帯域フィルタを通せば元の信号を再現できる．

(4)  FM変調ではスペクトルがの両側にの10倍以上の広がりを持つ．すなわちFM変調では広い帯域フィルタが必要である．