１０　スペクトル解析（２）−非周期波形のスペクトル−（10spectrum2）

・ 非周期関数も多くの振動数の重ね合わせからなる．

・ それぞれの振動数の振幅はいくらであるかを知るのがFourier変換（スペクトル解析）であり，それらの振動を合成して（重ね合わせて）元の波形を再現するのがFourier逆変換である．

・ このシミュレーションンでは，

（１） 非周期波形をFourier変換して，スペクトルを求める．

（２） 有限のスペクトル成分の振動を合成して元の波形を再現する．

・ スペクトルの全ての正弦波を合成すれば少なくともTまでの元の波形が再現できる．もし有限のスペクトル正弦波を合成すれば波形がどのように歪むかを調べる．

・ 非周期波形のFourier変換（スペクトル解析）

非周期波形をとするとスペクトルは理論的には

　　　（単位は振幅密度でm/(rad/s)）

　，　　

であるが，有限時間をとれば

，　　

　，　　

である．Tより先のが十分小さければを滑らかにつないだ曲線はとほとんど同じになる．

・ 有限スペクトルの合成（Fourier逆変換）

再生波形は，理論的には

　　

であるが，有限時間スペクトルを有限個とって合成した波形は

　　

　　とする（実際の計算では台形則を使う）．

● シミュレーションにおける描画画面

・ 画面左側　：　原非周期波形と有限数スペクトルを合成した再現波形

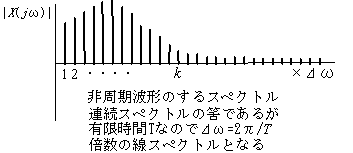
左側　：　スペクトル（刻みの線スペクトル）

● シミュレータの使い方

・ スタート → (1)非周期波形の選択 → (2)波形合成するスペクトル数設定 → 描画

・ キー操作（描画画面上でキーを押し，変更は文字画面上で）

m　　：別の波形選択（自作の周期データを使うこともできる）

n　　：合成スペクトル数変更

t, T　：波形の時間軸拡大縮小

y, Y　：スペクトルの縦軸拡大縮小

x, X　：スペクトルの横軸拡大縮小

●　特徴

(1)  滑らかで早く０に収束する波形ほどスペクトルも早く小さくなる．

(2)  T以上でも０に収束しない波形のスペクトルは真のスペクトルと異なる．

(3)  この場合でも十分多いスペクトルの合成による再生波形は元の波形と同じになる．

(4) のようなで急に立ち上がる波形は，かなり多くのスペクトルをとらないと，その立ち上がりと．の付近で誤差が大きい．