１１　線形１自由度振動系のランダム振動（11Randomvib）

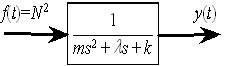・ １自由度振動系のランダムノイズに対する応答を求め，入出力のスペクトルと系の周波数特性（伝達関数）を求める．

・ データ数を増すことによって如何にスペクトル・周波数特性が理論値に収束するかを見る．

・ 「第１２節相関関数とパワースペクトル」のケースと比較して，単純な応答のスペクトルから信頼性のある系の特性が得られるかどうか調べる．

・ 振動方程式は

　　

　　，，と置くと

　　

　　入出力をFourier変換すると，周波数特性は

　　　　　　　

　　である．

●　シミュレーションンにおいて

・ 入力は平均振幅の一様分布ランダムノイズである（正規分布ではない）．

・ ランダムノイズに対する応答を微分方程式を解いて求める．

・ 入出力を適当な時間だけとってそれぞれをFourier展開する．

　　，　

　　

　

・ この応答をとって，を求める操作をnav回繰り返し，その平均値を求める．

　　，　

　　理論的にはである．

・ 系の周波数特性を計算する．

振幅特性　：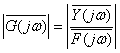　

位相特性　：　

・　この推定特性は元の１自由度振動系の周波数特性と一致しなければならない．

●　シミュレーションの描画画面

　　画面右側：振動の時間経過

　　　　左側：（ａ）入出力の平均スペクトル，

　　　　または（ｂ）伝達関数（振幅と位相の周波数特性），

●　シミュレータの使い方

・　スタート　→ (1)（文字画面で）入力　→ (2) 外力平均振幅入力

→ (3) データの平均回数nav入力 → 描画画面表示

・ キー操作：描画画面において

　s　　 ：外力ノイズと応答曲線

　　　　m　　：系のパラメータ変更（文字画面で入力）

　　　　n　　：平均回数nav変更（文字画面でnav入力）

　　　　f or g ：スペクトルまたは周波数特性描画の選択

●　特徴

(1) データ取得回数navを多くするに従ってスペクトルのばらつきが小さくなる様子が見られる．

(2) 伝達関数の振幅特性は取得回数が少なくても理論値に近い値になっている．取得回数を増しても改善されるわけではない．

(3) 位相特性は誤差が大きく，取得回数が多くなっても改善されない．

(4) すなわち，伝達関数の振幅特性だけを知りたければ，１回のデータ取得で十分信頼できる結果を得ることができるが，位相特性は回数を増やしても知ることはできない．

(5) 「第１２節相関関数とパワースペクトル」では取得回数を増す程伝達特性の信頼性が増す点で異なる．