１２　相関関数とスペクトル密度（12correlation）

 

 

・         １自由度振動系のランダムノイズに対する応答を求め，入出力の相関関数・スペクトル密度などから系の周波数特性（伝達関数）を推定する．

・         データ数を増すことによって如何に各関数・周波数特性が理論値に収束するかを見る．

 

●シミュレーションンにおいて

・         振動方程式は正規化した形で（固有振動数）

　　

　　の微分方程式よりランダムノイズに対する応答を求める．

　　入出力をFourier変換すると，周波数特性は

　　　　　　　

　　である．

・         相関関数は，外力の自己相関関数

　　

　　応答の自己相関関数

　　

　　外力と応答との相互相関関数

　　

　　を求める．

　　最大ラグ時間（データ長は必要）なので，最小振動数はである．またで離散化しているので，最大振動数はである．（このシミュレータではn=250，m=200，としており，最大振動数，時間刻み，最大ラグ時間である）

・         スペクトル密度，

(1)       外力のパワースペクトル密度

　　    

　　(2) 応答のパワースペクトル密度

　　   

　　(3) 相互スペクトル密度

　　   

　　　　を求める．

    　　w(t)はWindowでDo-Nothing window,  Bartlett winodwのどちらかを使う．

　　(4) 生データのスペクトル

外力の振幅スペクトル　 

　　　　応答の振幅スペクトル　  

　　　　を求める．

・　周波数特性（系の伝達特性）

(1) 入出力のパワースペクトル密度の比から　

　　(2) 振幅スペクトルの比から　　　　

    (3) 相互スペクトル密度から（１）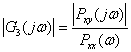　

，　

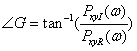    (4) 相互スペクトル密度から（２）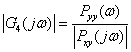　

　　を推定する．

・　入出力間のコヒーレンシ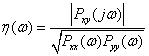         

　　を求める．

・         外力は白色ノイズ，１次遅れ要素(白色ノイズのLPF通過出力)の２種類

・          

●          シミュレーションにおける描画画面

　　画面左側：相関関数と入出力の時間変化，

右側：スペクトルまたは推定周波数特性　を表示．

 

●          シミュレータの使い方

 

スタート　→ (1)（文字画面で）ζ入力　→ (2) 外力種類の選択　→ (3) Windowの選択

→ 描画画面表示

　　　キー操作：描画画面において

　　　　　　m　　：系のパラメータζ変更

　　　　　　f　　 ：外力種類変更（白色ノイズ’w’か１次遅れノイズ ‘l’ か）

            w    ：Window変更（Do-Nothig Window ‘d’かBartlett Winodw ‘b’か）

　n　　 ：データ取り込みと平均化計算，結果を描画

　　　　　　g or p ：スペクトルまたは周波数特性描画の選択

　　　　　　t or T ：相関関数・生データの時間軸縮小拡大

　　　　　　y or Y ：スペクトル・相関関数・生データの縦軸倍率縮小拡大

　　　　　　z or Z ：スペクトルの横軸縮小拡大

　　　　　　ESC　：終了

 

●　特徴

(1)       データを多く取得するに従って相関関数・パワースペクトル密度が理論値に収束する様子が見られる．

(2)       相関関数の方がパワースペクトルより収束が早い．

(3)       相関関数の最大ラグ時間内で関数が0に収束しないと，スペクトル密度の高周波成分の誤差が大きい．すなわち，系の減衰比が小さいと（ζ<0.2）内で関数が収束せず，高周波でギザギザになっている．

(4)       Do-Nothing windowではスペクトルのばらつきが大きいがBartlett windowでは滑らかでばらつきが小さい．

(5)       各スペクトルはデータ収集量を増やしても収束が遅いが，そのスペクトルから計算した周波数特性（系の伝達特性）は収束が早い．

(6)       coherencyはほとんど１である．すなわち入出力間の因果関係が非常に強い．スペクトルはデータが少ないとばらつき大きいが，振動数の入出力比は因果関係が強いのでばらつき小さく一定であり，周波数特性は滑らかである．因果関係が強い入出力関係の系では，周波数特性を知りたいとき多くのデータを取る必要がない．

(7)       自己相関関数から求めたパワースペクトル密度と，生のデータをFourier変換した振幅スペクトルとほとんど変わらない．参考書には後者はばらつきが大きいので使わない方がよいとあるが，実用上は差し支えない．後者の方が計算量が少ないので（相関関数計算が不要），スペクトルや周波数特性（伝達関数）を知りたいときはこちらを利用した方がよい．

(8)       相互スペクトル密度とパワースペクトル密度から伝達特性の位相遅れを求めることができる．ただし結果にやや偏りが見られる．その原因は分からない．

(9)       白色ノイズのスペクトル密度は理論的には０である．実際には振動数を限っている（最大振動数）ので，帯域制限白色ノイズとなり，スペクトル密度は＝一定である．

(10)帯域制限ノイズに対する応答は，Ωを越えて意味のある振動数があればその振動数のスペクトル・周波数特性が得られないだけでなく，Ω以下の振動数特性にも影響する．LPFノイズに対するシミュレーションで時定数τが大きいときにその影響が見られる．

(11)このことからも，サンプル時間は少なくともであることが望ましい．