１３　非線形系の自由振動−位相平面解析−( 13Phaseplane )

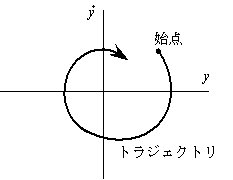
・１自由度振動系の振動を位相平面に描き，同時に変位速度の時間変化を示す．

・位相平面の横軸は変位，縦軸は速度である．

・各種振動系の振動のトラジェクトリを表示するが，どの場合も振動方程式を正規化している．

●　シミュレーションする振動系

１３．１．１自由度減衰自由振動

　　

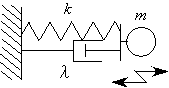
正規化して

　　

・　トラジェクトリの特徴は

　ζ<1のとき，傾いた渦巻き状になる．

　ζ>1のとき，原点に単調に近づく．

　異なる初期値から出発するトラジェクトリは決して交わらない．

　Ｘ軸と直角に交わる．

１３．２．ガタのある１自由度減衰振動系

　　

正規化して

　　

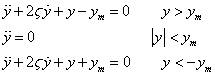
・　の外でばね力が作用し，範囲内では自由に運動する系である．

・　トラジェクトリは振幅が小さくなるほど往復時間が長いことがわかる．

１３．３．予圧ばねによる１自由度減衰振動系

　　

　　

・　は予圧によるばねの撓みを表す．

１３．４．左側に壁のある１自由度減衰衝突振動系

　　

正規化して

　　

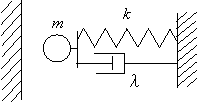
のとき　　

・　壁がの位置にあり，壁で反発係数eで跳ね返る．

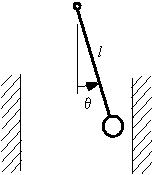
１３．５．呼び鈴のスイッチの運動

　　

正規化して

　　

のとき　　

・　ベルがの位置にあり，ばね付きの電気接点が鈴に接触した瞬間に電気的に通電しコイルからの力積を得る．その力積による速度と反発係数eによる跳ね返り速度が加算されて跳ね返りの速度となる．

・ コイルの強さ（力積）によってベルの１周期が決まる．

・ 力積が小さいとベルは鳴らない．力積が大きくなると周期は早くなるがその変化は小さい．

・ ベルが遠いとベルは鳴らない．また鳴っても周期が遅い．

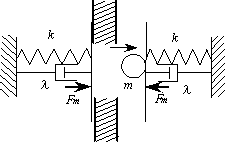
１３．６．左右両側に壁のある１自由度減衰衝突振動系

　　

正規化してと置くと

　　

のとき　　

のとき　　　　　　　　　　　　　　　　　　　　　　　　　　気体の粘性摩擦係数λ

・　壁がの位置にあり，壁で反発係数eで跳ね返る．

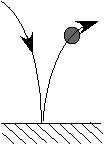１３．７．重力による床からの跳ね返り運動

　　

正規化して

　　

のとき　　

気体の粘性摩擦係数λ

１３．８．左側に壁のある１自由度強制衝突振動系

　　　　

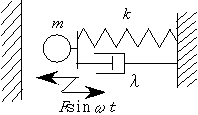
正規化すると

　　

のとき　　

・　壁がの位置にあり，壁で反発係数eで跳ね返る．

・　衝撃による鍛造や，金箔の製造などの機械の動作をシミュレーションしている．

・ 安定な衝突振動が得られないケースが多い．

・ z=2（固有振動数の２倍の強制振動数）では安定な振動が得られる．

・ 壁の位置・強制振動数・反発係数などによって安定振動の条件が変わり，傾向を知るのが難しい．

１３．９．Val der Polの式

　　　

・　典型的な自励振動（弛緩振動）のタイプである．

・　Karmanの渦，旗のはためき，自動車のシミー，ドアのきしみ，フルート・クラリネット・トランペットなどの吹奏楽器の発音など振動的な力がないのに振動が生じる現象はこの自励振動によるケースが多い．

・　どんな初期条件から始まっても安定な定常振動に収束する．

・ ε<<1のときは振動はほぼとなる．

・　ε>>1のときは周期が長くなり矩形波に近い波形となる．

１３．１０．Mathieuの式（係数励振型自励振動）

　　

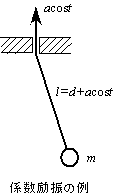
・　εが大きいと振動は発散する（不安定）．

・ β=0のとき，εが小さいと振幅は一定範囲内に納まるが，周期的な振動とは限らない（安定，Lyapunovの意味の安定）．両者の境界では周期1/(2π)または1/(4π)の周期振動が生じる筈だが，定常的な周期振動を実現する初期条件を設定するのが難しい．

・ β≠0のとき，安定とは０に収束を，不安定とは発散を意味し，両者の境界では周期1/(2π)または1/(4π)の周期振動が生じる．例えばβ=0.1，δ=1のとき，ε=1.07で周期1/(2π)の定常振動が得られ，β=0.2，δ=4のとき，ε=5.88で周期1/(4π)の定常振動が得られる．

・ δ<0でも,δが小さくてεを適当な値にすれば振動が発散しないことがある．すなわち，δ<0では本来発散するが，係数を周期的に変化させれば安定にすることができる．

・　振動が発散するかどうかについては，１７．係数励振型自励振動の項で論じる．

１３．１１．矩形波係数励振型自励振動

　　

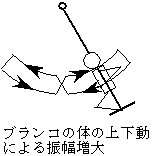
・ ブランコの運動（体重を上下させると振幅がだんだん大きくなる現象）

はこのタイプの係数励振型自励振動である．

・　この系の特質はMathieu型と同じである．

・　例えば，β=0.2，δ=4のとき，ε=3.71で周期1/(4π)の周期振動が得られる．

● シミュレーションにおける描画画面

　　　画面左側：振動曲線（変位・速度振動）

　　　右側：位相平面とトラジェクトリ

● シミュレータの使い方

・　スタート → (1)振動系の選択 → (2)系の定数設定 → (3)初期条件設定 → 描画

・　キー操作：描画画面において

s　　：振動継続（押さない限り動かない）

k    ：シミュレーションする振動系変更

m   ：系の定数変更

j    ：初期条件変更

T, t  ：時間軸拡大縮小

Y, y ：振動曲線縦軸・位相平面縦横軸拡大縮小