１５　Duffingの式（15Duffing）

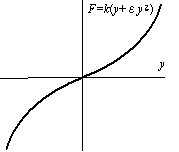
　・（正規化）方程式

　　　　

● シミュレーションにおける描画画面

　　　画面左側：振動曲線（外力と応答）

　　　　　右側：ζをパラメータとする周波数特性群

　　　　　　　　または外力Ｆをパラメータとする周波数特性群周波数特性（キーで選択）

　　　　　　　　応答曲線のスペクトル（’a’キーを押したとき）

● シミュレータの使い方

・　スタート　→ (1)（文字画面で）ζ，ε入力　→ (2) F，z入力　→ (3) 初期条件入力

→　描画画面表示

・ キー操作：描画画面上で

　s   ：振動の時間変化（押さなければ静止したまま）

m  ：系の定数ζ，ε変更

f   ：外力条件F，z変更

j   ：初期条件変更

y, Y ：振幅を縮小拡大する（１回毎に変更）

t, T ：時間軸縮小拡大（１回毎に）

e, E ：ζ可変or外力Ｆ可変の周波数特性群描画

a   ：波形のスペクトル表示（振動波形が１周期以上表示されたときのみ可）

ESC：終了

●　特徴

　ε＞０として

    (1) 共振点はｚ＝１でなく，高い方へずれる．

(2) ｚ＞１で２通りの安定な応答が得られる．

(3) 初期条件を小さくとると小さい振幅の応答が，大きいと大きい振幅の応答が得られる．

(4) ζ≪１のときｚ＝３の付近で，１／３次の分数次調波が生じることがある．

ただし，この応答を得る初期条件の設定が難しい．

(5) ｚ＜１では，高調波成分が顕著である．

　ε＜０のとき

(1) ばね定数が（正規化して）となることがあれば，この系は不安定である（指数的に大きくなる）．

(2) が小さくても，外力の振動数が低いとき不安定になることがある．振動数が十分高いときは安定な定常振動が生じる．

(3) 振動数が低い領域の周波数特性は描画されているが，信頼できない．

未知の系の共振周波数を知りたい場合に，強制振動の周波数を低い方から徐々に上げて，振幅が最大になる点を調べる方法がある．この方法で，最大振幅から急にがくんと落ちることを経験することがある．またこのとき周波数を大きい方から徐々に下げると最大振幅を示す周波数が上げる場合と異なる．これは全てばね性が非線形だからである．

　分数次調波は滅多に生じないが，実際の機械・システムで生じていれば，ばねの非線形性を疑うべきである．